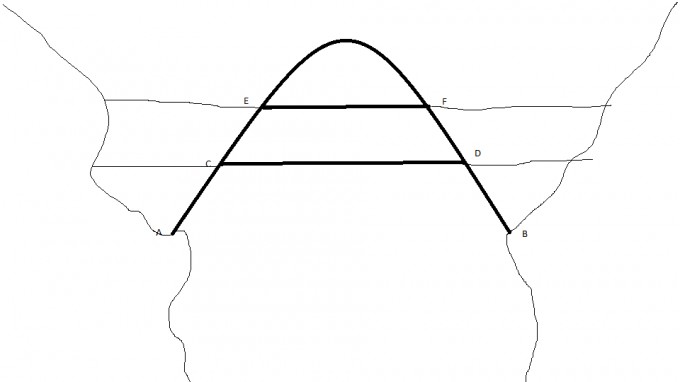
Eine Hängebrücken führt über eine Schlucht. Der stählerne Brückenbogen trägt zwei übereinander liegende, an Stahlseiten hängende Fahrbahnen, eine für Züge und eine für Autos. Der Brückenbogen kann durch eine Polynomfunktion vom Grad 2 beschrieben werden, wobei gilt:
Der Abstand der beiden Auflagepunkte A und B beträgt 50m.
Der höchste Punkt des Brückenbogens liegt 30m über der horizontalen Verbindungsstrecke der Punkte A und B.
Das längste Halteseil, das die Zugfahrbahn trägt, hat eine Länge von 19,2m
Die Länge der Autofahrbahn innerhalb des Brückenbogens (dh. von E bis F) beträgt 30m.
Die Funktiongleichung: ax²+bx+c und c ist 30, aber wie komme ich auf a und b?