Betragsungleichung ausrechnen

Question

Ich muss eine Betragsgleichnung ausrechnen:

Habe ich bei Schritt 1 und Schritt 2 etwas falsch gemacht?

Schritt 3 schaffe ich nicht! Die Lösung sollte sein L={x∈R / -4≤x<4}. Wie mache ich das? Es sollte ja so weit ich weiß eine ODER Verknüpfung sein  kann ich dann auch einfach schreiben L={x∈R / (-4≤x<-2) ∨ (-2≤x≤4)}. Was genau bedeutet so eine Oder Verknüpfung?

Bitte um Erklärung :) Danke

Answer 1

Ich komme auf die Lösung:

-4 ≤ x ≤ 4

Sorry. Hatte einen Fipptheler.

Comments

Das ist leider falsch... Die Lösung L={x∈R / -4≤x<4} ist ganz sicher richtig. 

Bitte um Lösungswege!!! 

---

1/2·|x + 2| ≤ 0.25·x + 2

Fall 1: x ≤ -2

1/2·|x + 2| ≤ 0.25·x + 2

0.5·(-(x + 2)) ≤ 0.25·x + 2

- 0.5·x - 1 ≤ 0.25·x + 2

- 0.75·x ≤ 3

x ≥ -4 und x ≤ -2 --> -4 ≤ x ≤ -2

Fall 2: x ≥ -2

1/2·|x + 2| ≤ 0.25·x + 2

0.5·(x + 2) ≤ 0.25·x + 2

0.5·x + 1 ≤ 0.25·x + 2

0.25·x ≤ 1

x ≤ 4 und x ≥ -2 --> -2 ≤ x ≤ 4

Vereinigung der Lösungen

-4 ≤ x ≤ -2 oder -2 ≤ x ≤ 4

-4 ≤ x ≤ 4

---

Ein ODER bedeutet du sollst hier die Vereinigungsmenge der beiden Lösungsmengen nehmen.

Es gehört alles in die Vereinigungsmenge was in einer Menge oder in der anderen drin ist. Natürlich auch das was in beiden drin ist. Das mathematische oder ist kein entweder oder.

Answer 2

Deine Berechnungen für Fall 1 und 2 haben keine Fehler.

Am besten du malst dir die Lösungen immer auf einem Zahlenstrahl ein




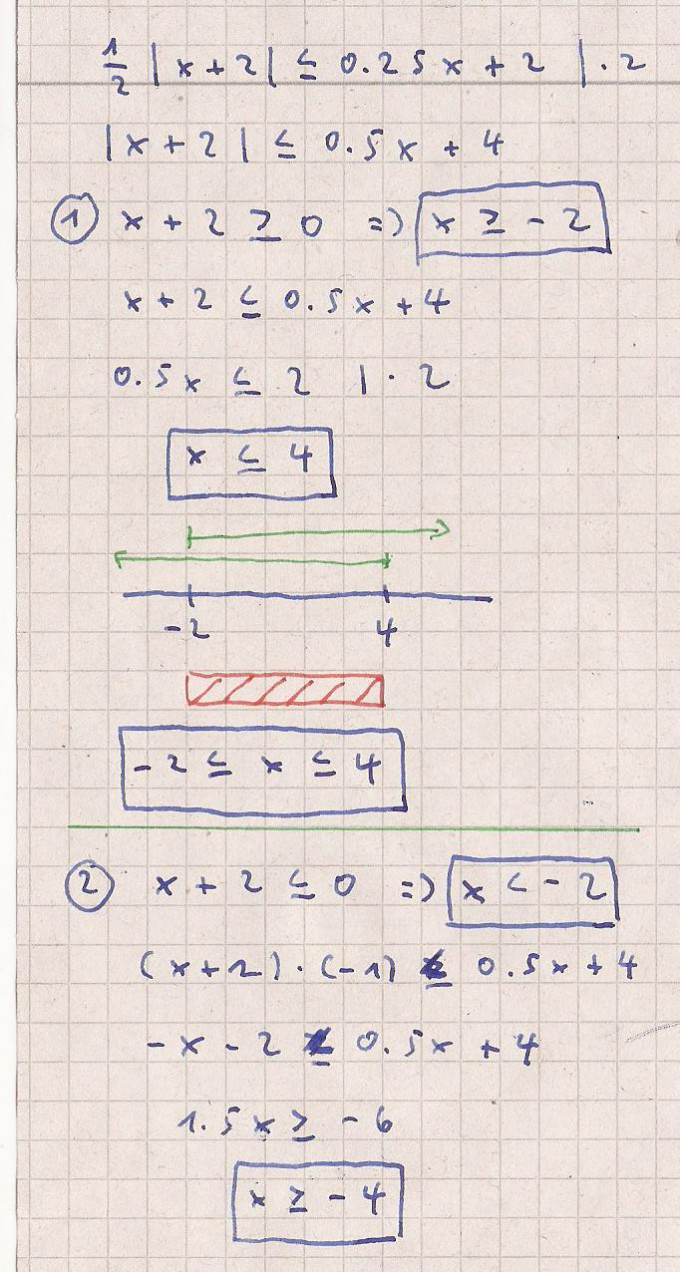
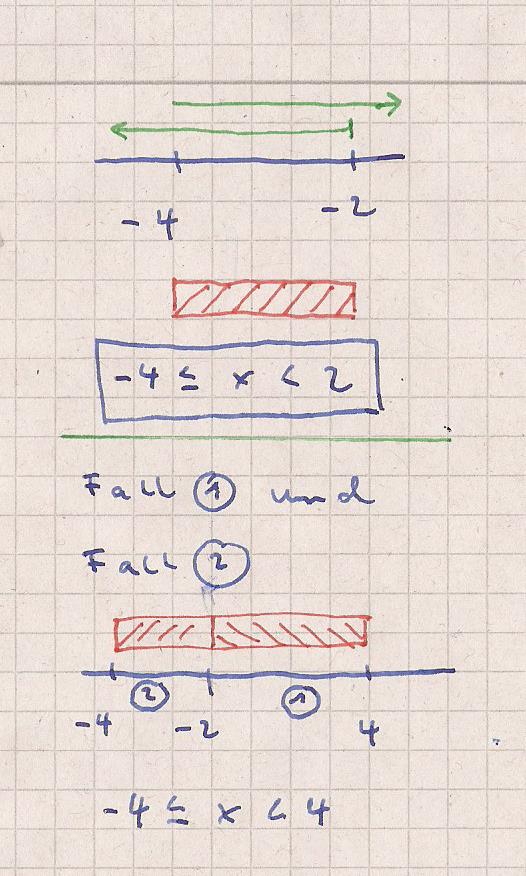
In Worten bedeutet die Lösung :
Wenn eine Zahl x im Zahlenbereich von Fall 1 ist
oder im Zahlenbereich von Fall 2 ist dann gehört
sie zur Lösung.

Wobei der Gesamtzahlenbereich sich in dieser Rechnung zu
-4 ≤ x ≤ 4
ergibt.