Betragsungleichung: | 4 - 3x | ≤ 6 . Wie kommt man auf die Lösung?

Question

Betragsungleichung: | 4 - 3x | ≤ 6

\( |u-3 x| \leq 6 \)
\( 4-3 x \leq 6 \)
\( 4-6 \leq 3 x \)
\( 2 \leq 3 x \)
\( \frac{2}{3} \leq x \)

Lösung ist \( -6 \leq 4-3 x \leq 6 \)

Wie kommt man auf -6 < 4-3x < 6?

Answer 1

Bereits die erste umformung ist ja schon verkehrt. Man darf in einer Ungleichung nicht einfach die Betragsstriche weglassen.

Schauen wir uns mal

|z| ≤ k an

Da |z| nicht negativ ist muss k in diesem Fall auch positiv sein. Jetzt könnte man eine Fallunterscheidung machen.

Fall 1: z ≤ 0

-z ≤ k
z ≥ -k

Fall 2: z ≥ 0

z ≤ k

Das kann man auch in einer Gleichung zusammenfassen

|z| ≤ k
-k ≤ z ≤ k

In dieser Gleichung sind jetzt die beiden Fälle vereint.

Wenn du das jetzt auf deine Ungleichung anwendest sollte es klar sein.

|4 - 3x| ≤ 6
-6 ≤ 4 - 3x ≤ 6
-10 ≤ - 3x ≤ 2
-2/3 ≤ x ≤ 10/3

Und das ist jetzt auch erst die Lösung.

Answer 2

Wenn Du zeigen willst, dass es eine Cauchyfolge ist, musst Du uns auch die Folge beschreiben.

Answer 3

Alle Zahlen von -6 bis +6 haben einen Betrag, der kleiner gleich 6 ist. D.h. 4-3x muss zwischen-6 und +6 liegen.

Answer 4

Betragsungleichung: | 4 - 3x | ≤ 6

Wie kommt man auf -6<4-3x<6?

Betragszeichen, heissen nichts anderes, als dass man das Vorzeichen weglässt.

Graphisch hast du

~plot~ abs( 4 - 3x); 6 ; 4 - 3x ; - 6 ;[[-1|10|-10|10]] ~plot~

~plot~ abs( 4 - 3x); 6 ; 4 - 3x ; - 6 ;[[-10|10|-10|10]] ;x=-2/3;x=3+1/3 ~plot~

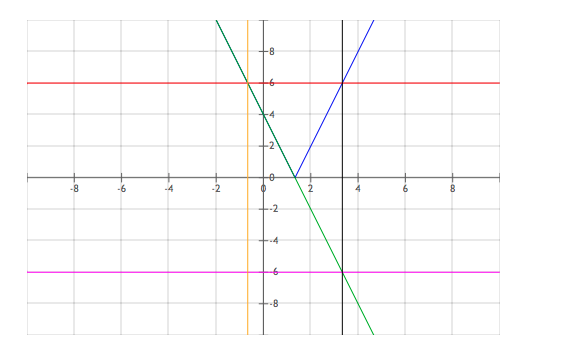
Blende wahlweise das blaue v oder die grüne Gerade aus.

Du suchst den Bereich, in dem das blaue v nicht über y=6 liegt.

Das ist dasselbe wie der Bereich in dem die grüne Gerade den Bereich von -6 ≤ y ≤ 6 nicht verlässt.

Answer 5

\( |4-3 x| \leq 6 \)
\( \sqrt{(4-3 x)^{2}} \leq\left. 6\right|^{2} \)
\( (4-3 x)^{2} \leq 36 \)
\( 16-24 x+9 x^{2} \leq 36 \)
\( 9 x^{2}-24 x \leq 20 \)
\( x^{2}-\frac{8}{3} x \leq \frac{20}{9} \)
\( \left(x-\frac{4}{3}\right)^{2} \leq \frac{20}{9}+\frac{16}{9}=\left.4\right|^{\frac{1}{2}} \)
1.) \( x-\frac{4}{3} \leq 2 \)
\( x_{1} \leq \frac{10}{3} \)
2.) \( x-\frac{4}{3} \leq-2 \)
\( x_{2} \geq-\frac{2}{3} \)
\( -\frac{2}{3} \leq x \leq \frac{10}{3} \)