Steckbriefaufgabe: Graph einer ganzrationalen Funktion dritten Grades berührt die x Achse an der Stelle x= -2 mit ..

Question

kann mir jemand diese aufgabe lösen

Der Graph einer ganzrationalen  Funktion dritten Grades berührt die x Achse an der Stelle x=-2 mit der Krümmung -2,5. Die Tangente im Punkt P(3/f(3)) hat die Steigung 6,25. Wie lautet der Funktionsterm?

Comments

EDIT: Dieser Aufgabentyp wird oft "Steckbriefaufgabe" genannt. Habe Begriff in deine Fragestellung integriert. 

Es gibt eine ziemliche Rechnerei. Lass dich schon mal bei den "ähnlichen Fragen" inspirieren, bis jemand genau deine Aufgabe gerechnet hat.

Answer 1

Hallo Nadin :-),

f(x) = ax³ + bx² + cx + d          [ Normalform ]

f(x) = a • (x + 2)² • (x - n)          [ Nullstellenform ]

( Nullstellenform,  x = -2 ist doppelte Nullstelle [ berührt x-Achse ], Nullstelle n noch nicht bekannt )

f ''(-2) = -2,5                               ( Krümmung f ''(x)  = -2,5  an der stelle  x = -2 )

f '(3) = 6,25                                ( Steigung f '(x) = 6,25 an der stelle x = 3 )

f '(x) und f ''(x) ausrechnen und das Gleichungssystem mit zwei Unbekannten lösen:

f '(x) =  a·(x + 2)·(3·x - 2·n + 2)

f ''(x) = 2·a·(3·x - n + 4) 

f '(3) =  5·a·(11 - 2·n)  =  6.25   G1

f ''(-2) =  - 2·a·(n + 2)  =  -2.5     G2

G1/G2:   -2,5 • ( 11 - 2n) / (n+2) = -2,5  →  11 - 2n = n + 2 → n = 3

n in  G2 →  -10a = -2,5  →  a = 1/4

a,b   einsetzen in   f(x) = a • (x + 2)² • ( x - n)    [vgl. Antwort]

f(x) = 1/4 • (x+2)² • (x-3)         [ Nullstellenform ] 

ausmultiplizieren:

 f(x) = 1/4 • x³ + 1/4 • x² - 2 • x - 3      [ Normalform ]

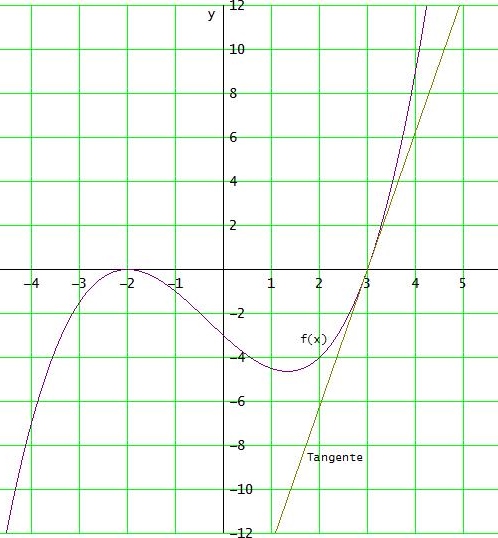
Gruß Wolfgang

Comments

Kannst du bitte die koffezienten auch bestimmen ?

Meine ich a, b, c, d 

Und ist in diesem Fall f(-2)=0 ?? 

 

---

a=1/4 , b = 1/4 , c = -2  , d = -3

Habe die Antwort diesbezüglich ergänzt, schau mal dort.

> Und ist in diesem Fall f(-2)=0 ?? 

ja, x = -2 ist sogar eine doppelte Nullstelle, deshalb hast bei der Nullstellenform nur 2 Unbekannte.

Answer 2

Der Graph einer ganzrationalen  Funktion dritten Grades

f ( x ) =  a * x^3 + b * x^2 + c * x + d
f ´( x ) = 3 * a * x^2 + 2 * b * x + c
f ´´ ( x ) = 6 * x + 2 * b

berührt die x Achse  an der Stelle x=-2
f ( -2 ) = 0
f ´( -2 ) = 0

mit der Krümmung -2,5.
f  ´´ ( -2 ) = -2.5

Die Tangente im Punkt P(3/f(3)) hat die Steigung 6,25.
f ´( 3 ) = 6.25

Wie lautet der Funktionsterm?

Gleichungssystem aufstellen d.h. die Werte in die Gleichungen
einsetzen z.B.
f ( x ) =  a * x^3 + b * x^2 + c * x + d
f ( -2 ) =  a * (-2)^3 + b * (-2)^2 + c * (-2) + d = 0
-8·a + 4·b - 2·c + d = 0
und berechnen.

Zur Kontrolle
-8·a + 4·b - 2·c + d = 0
12·a - 4·b + c = 0
-12·a + 2·b = -5/2
18·a + 2·b = 25/4

f ( x ) = 7/24·x^3 + 1/2·x^2 - 3/2·x - 8/3

~plot~ 7/24 * x^3 + 1/2 * x^2 - 3/2 * x - 8/3 ~plot~

Comments

Hallo Georg,

> mit der Krümmung -2,5. 
> f  ´´ ( 2 ) = -2.5  

muss wohl

f  ´´ ( - 2 ) = -2.5  heißen    Gruß Wolfgang

---

Hallo Wolfgang,
danke für den Hinweis.
Bin gerade mit dem korrigieren fertiggeworden.

mfg Georg

---

f ( x ) = 7/24·x³ + 1/2·x² - 3/2·x - 8/3  →  f(3) = 125/24

→  t(x) = 6.25*(x-3) + 125/24

irgendetwas stimmt da nicht:

deine Tangente würde so aussehen

mfG Wolfgang

---

Hallo Wolfgang,
nochmals Danke.

Es muß heißen
-8·a + 4·b - 2·c + d = 0
12·a - 4·b + c = 0
-12·a + 2·b = -5/2
27·a + 6·b + c = 25/4

f(x) = 0,25·x^3 + 0,25·x^2 - 2·x - 3

---

Hallo Georg,

> f(x) = 0,25·x³ + 0,25·x² - 2·x - 3

stimmt mit meiner Antwort überein, was mich sehr beruhigt :-)

Gruß Wolfgang

---

@Wolfgang

Für deine Hinweise gibt es zur Erheiterung 3 Stilblüten
aus dem Matheforum

Ich muss immer mueh srlig i2 machen und dann einzelnd kann ich nicht
irgwie i8 i machen?

Ableitung von Wurzel(x)
In dr letzen frage hatte ich gefrakt mit Wurzel x. Aber wiso ist Wurzel x
denn das uebehaupt??? Wie leitet Mann das ab?!

Ich weiß, dass man immer für x das einsetzt gegen was das laufen soll und wenn
nicht 0 rauskommt ist man fertig."