Term vereinfachen mit Fakultät

Question

Könnt ihr mir helfen diesen Term zu vereinfachen?

((2n-5)! + (4n-8)!) / ((7-2n)! - (5-2n)!)

Comments

Und was soll \(n\) sein? Dein Ausdruck ist für kein \(n\in\mathbb{N}\) definiert.

---

@döschwo:

Du musst mir mal verraten, wie man einen Kommentar oder eine Antwort unter 12 Zeichen überhaupt absenden kann :-)

---

Die definitionsmenge von n sind alle reellen zahlen

---

Meine Frage war durchaus  ernsthaft gemeint. Wenn ich einen Kommentar lösche, muss ich immer irgendwelche 12 hässliche Zeichen hinschreiben ??

---

@Wolfgang: Du solltest einen Button "Ausblenden" ganz rechts sehen. Diesen einfach drücken:

Answer 1

Bist Du sicher, dass die Aufgabe so lautet?

Allein der komplexe Kurvenverlauf mit zig Polstellen kann doch mit keiner "noch einfacheren" Funktion abgebildet werden...

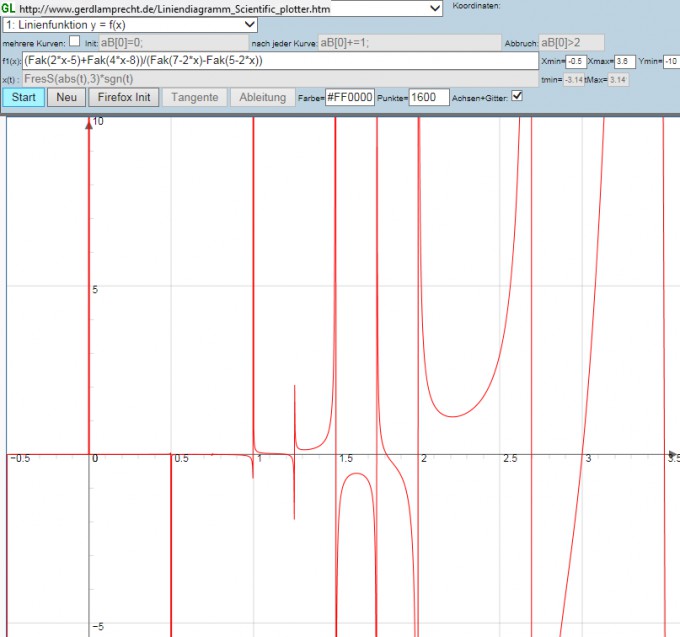
Natürlich kann man alles in Gammafunktion, Pochhammer-, oder hypergeometrischen Funktionen umschreiben, aber das sieht dann noch komplizierter aus...

Bei Fakultätsfunktion kann man nur vereinfachen, wenn Produkt- oder Divisions-Operatoren beteiligt sind. Bei Dir werden aber Additions- & Subtraktions-Operatoren verwendet -> Schreibfehler?

Klammerfehler?

Comments

interessant, man kann von 4 auf 3 Funktionen reduzieren:

((2n-5)!+(4n-8)!)/((7-2n)!-(5-2n)!) = (Γ(2n-4)+Γ(4n-7))/((41-26n+4n^2)Γ(6-2n))

={(3-n)[(2n-4)!+(2n-4)(4n-8)!]}/((n-2)(4n²-26n+41)(6-2n)!)

---

Oder sollt Ihr nur ganze Zahlen betrachten, denn aus Sicht vieler Lehrer ist Fakultät nur für ganze Zahlen definiert :-)

Dann schau Dir weitere Umformungen an unter

http://www.lamprechts.de/gerd/nichttrivialeGrenzwerte_Limes.html

§39

sieht man sofort, dass sin(2* Pi * n) bei ganzzahligen n -> Nullstellen ergibt

ABER Polstellen (also alles n < 3 ) ausklammern!

---

Die Fakultaet ist sicher nicht für ganze Zahlen definiert, da die Gammafunktion an negativen ganzzahligen Stellen einen Pol hat. In diesem Sinne: Gib ein ganzzahliges n an, für das sowohl (2n-5)! als auch (5-2n)! definiert ist. Die ganze Aufgabe ist Bloedsinn, wahrscheinlich vom Fragesteller selbst erfunden.

---

Zwar sind die Teilfunktionen nicht definiert, ABER es gibt so etwas wie "hebbare Polstelle"

( http://www.frustfrei-lernen.de/mathematik/definitionsluecke-hebbar-pole-nullstellen.html

)

für n>=3

und auch bei WolframAlpha kommt ab x=3 das Ergebnis 0 raus:

https://www.wolframalpha.com/input/?t=elg01&i=((2n-5)!%2B(4n-8)!)%2F((7-2n)!-(5-2n)!),n%3D3

und alle 3 Funktionen (die ersten 2 mit Limes-Tricks, aber die letzte ohne Tricks)

unter §39 kann man plotten und sie gehen ab n=3 sauber (knick-frei) durch die x-Achse...