 So, in der Musterlösung steht folgendes:
So, in der Musterlösung steht folgendes:
1.Listen sie alles vorgegebenen Änderungsraten und die zu berechnende Änderungsrate auf:
$$ \frac{dh}{dt}=15 m/s \\ \frac{dd}{dt}=? $$
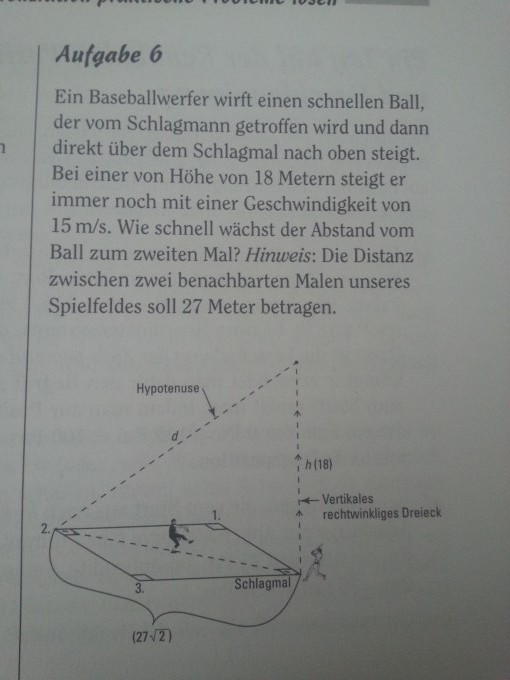
2. Schreiben sie ine Formel, in der die Variablen enthalten sind: $$ h^2+(27\sqrt{2})^2=d^2 $$
3. Differenzieren sie nach der Zeit: $$ 2h\frac{dh}{dt}=2d\frac{dd}{dt} \\ 18^2+(27\sqrt{2})^2=d^2 \rightarrow d=42,2 \\ 2h\frac{dh}{dt}=2d\frac{dd}{dt}~ \leftrightarrow ~\frac{dd}{dt}=\frac{2\cdot 18\cdot 15}{2\cdot 42,2} = 6,4 m/s $$
4. Ist diese Lösungs sinnvoll? Hinweis: Verwenden sie den Satz von Pythagoras, um d*1/50 Sekunden nach dem kritischen Moment zu berechnen. Erkennen sie warum ich diesen Zeitschritt gewählt habe?
Mein Problem liegt bei Schritt 3: Wenn ich diesen Term differenziere $$ h^2+(27\sqrt{2})^2=d^2 $$ erhalte ich: $$ 2h=2d $$ , aber doch nicht $$ 2h\frac{dh}{dt}=2d\frac{dd}{dt} $$ , dann würde ich doch noch ein weiteres mal differenzieren oder?
Nächstes Problem bei Nr. 4, dass richtige Ergebnis ist "die Distanz nimmt um 21,3 m/s zu", also stimmt 6,4 m/s wohl nicht und sein Hinweis scheint einen Grund zu haben, wie kommt man darauf?
Kann mir jemand bitte meine Frage zum 3. und 4. Punkt beantworten?