Mit Höchstpreis ist wahrscheinlich der Preis gemeint, über dem es keine Nachfrage mehr gibt. Der liegt bei 80, wird aber nie realisiert werden, weil die Nachfrage dann zu klein ist, dass jemand zu diesem Preis noch anbietet.
Angebot und Nachfrage sind identisch bei x = 34.34 (Gleichgewichtspreis) d.h. Sättigungsmenge 28.54
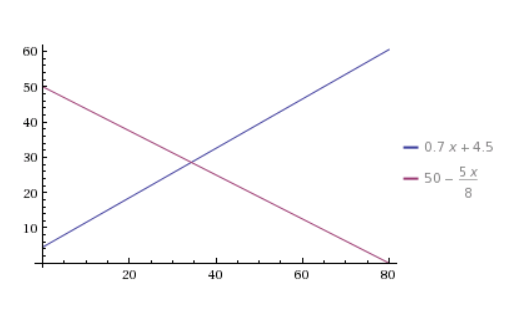
Lösungsweg: Setze die beiden Funktionen gleich, löse nach x auf, setze dieses x in beide Funktionen ein und beide ergeben eine Menge von 28.54