Für welche lambdas ist A diagonalisierbar?

Question

sei

A=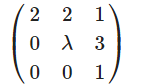   

Für welche \(\lambda\) ist A diagonalisierbar?

Ich weiss, dass f diagonalisierbar ist wenn V eine Basis von Eigenvektoren besitzt.

Oder dass A diagonalisierbar ist, wenn es \(\lambda_1,\lambda_2.......\lambda_r \in \mathbb{K}\) gibt mit der Summe der geometrischen Vielfachheiten=n.

Ich habe einmal das Charakteristische Polynom aufgeschrieben welches ja:

\((2-t)(\lambda - t)(1-t)\) ist. Also sieht man die drei Eigenvektoren. Wie kann ich nun aber herausfinden, was \(\lambda\) sein muss?

Comments

Tipp: Eigenvektoren zu verschiedenen Eigenwerten sind linear unabhaengig.

---

Ja aber dann könnte ich ja alles für Lamda nehmen ausser 2 und 1 oder?

---

Wieso ist 1 und 2 denn per se ausgeschlossen?

---

Tipp: Berechne die Dimension der Eigenräume in Abhängigkeit von  λ

---

Also 1 und 2 werden ausgeschlossen, da es dann 2 gleiche Eigenwerte hätte und somit nur 2 versch Eigenvektoren und dann könnte es keine Basis sein.

---

Die Eigenräume haben doch alle Dimension 1 hier oder?

Answer 1

Hi,

Für λ≠1 und λ≠2 ist die Matrix immer diagonalisierbar, weil es dann 3 versch. Eigenwerte gibt (das Maximum bei einer 3x3 Matrix) und somit jeder Eigenraum maximal dim=1 haben kann.

λ=1 und λ=2 kann man separat ausprobieren, da man dann jeweils einen doppelten Eigenwert bekommt müsste auch der dazugehörige Eigenraum die Dimension 2 haben, aber die Eigenräume haben nur Dimension 1. Daher ist die Matrix für diese beiden Fälle nicht diagonalisierbar.