Kreis ausrechnen Textaufgaben

Question

Ich habe leider Probleme bei diesen drei Textaufgaben... Könntet ihr mir bitte helfen? Trotz Formelheft komme ich nicht auf das richtige Ergebnis....

 

1) Eine Packung Rasensamen reicht für 7m². Ich möchte damit ein rundes Beet einsäen. Welchen Radius kann das Beet höchstens haben?

2) Ein Quadrat hat einen Flächeninhalt von 144cm². Es werden nun 4 Kreise ausgeschnitten. Wie viel Abfall entsteht?

3) Eine 435m lange Kurve in der Form eines Kreisbogens bewirkt eine Richtungsänderung von 180Grad. Skizziere den Sachverhalt. Wie groß ist der Radius? Überlege, wo die Länge einer Kurve gemessen werden kann?

Answer 1

1) die Fläche eines kreises wird berechnet mit A=π*r²

    gegeben: 7 m²

    umstellen nach r=√(7/π)=1,49

    Der Radius des Beetes ist 1,49 ≈1,5m

2.sind die Kreise gleichgroß , dann

   A= a²   Fläche des Quadrates , dann ist a=√144=12   ⇒  12cm

    jeder der vier Kresie hat dann einen maximalen Durchmesser von 6 cm, und einen Radiius von  3cm

    die Fläche der 4 Kreise ist dann

     A= 4(π*r²)=113,09

    Der Abfall : 144-113,09=30,91

    Der Abfall ist 30,91 cm² .

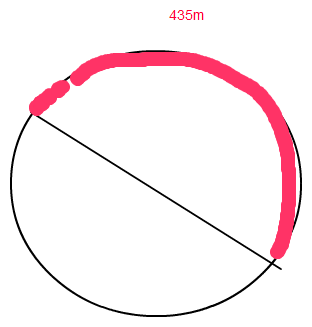
3.  435 ist der halbe Umfang eines Kreises

     U = 2* 435    U =2*π*r       r= U/(2π)

     r= 2*435/(2*π) = 138,46

   der Radius der Kurve ist 138,46 m.

Answer 2

Hi!

1) Die Fläche eines Kreises ist: pi * r^2 (r ist der Radius)

    Wir dürfen/können maximal 7 m^2 bepflanzen, also setzen wir pi * r^2 = 7 m^2 <=> r^2 = 7/pi m^2 => r = Wurzel(7/pi     m^2) = Wurzel(7/pi) m . das ist also der "maximale Umfang" (Das kann man natürlich runden usw.)

2) Diese Frage kann man so nicht beantworten, es werden nähere Info's zu den Kreisen benötigt.

3) Hier kannst du wieder mit Gleichungen (musst du wahrscheinlich) arbeiten, versuch's mal selbst...


gruß...