Differentialgleichung Lösung

Question

Hallo ich habe die Aufgabe :

mann soll hier zeigen dass x(t) eine Lösung von der Schwingungsgleichung ist.

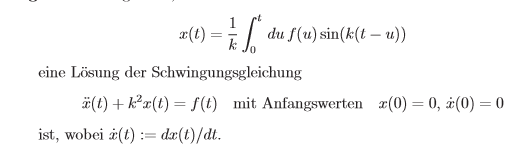
bei der ich mir schwer tue , da wir noch keine DGL dran hatten.

Ich hab mir im Internet durchgelesen es gibt eine DGl 2 Ordnung mit konstanten Koeffizienten , die hier denke ich beschrieben wird .

Da gibt es dann Homogene und Partikuläre Lösungen .

Was fange ich dann mit denen an und was machen die Anfangsbedingungen ? Muss ich die wo einsetzen oder so ?

Danke für Hilfestellungen !

Comments

Wie zeigt man, dass x=1 eine Lösung der Gleichung x²+x-2=0 ist? Man setzt ein und rechnet nach, dass es stimmt. Hier wird auch nichts anderes verlangt. So wenig wie man im Beispiel die pq-Formel zu kennen braucht, so wenig brauchst Du hier zu wissen, was du da alles zusammengegoogelt hast.

---

Hallo , wie würde das dann aussehen ? Kanst du mir eine Hilfestellung geben wie ich anfangen kann?

---

Na, Du rechnest \(\dot{x}\) und \(\ddot{x}\) aus und setzt das dann in \(\ddot{x}+k^2x\) ein. Rauskommen soll \(f\). Ausserdem sollst Du noch \(x(0)\) und \(\dot{x}(0)\) ausrechnen. Es soll in beiden Faellen 0 rauskommen. Das ist reines Nachrechnen. Geistesblitze werden nicht verlangt.

---

Ah ok so kann ich anfangen , bleibt nur noch die Frage wie leite ich dieses Integral ab wenn dort die variable im Integrationsbereich ist ?

---

Damit:

https://de.wikipedia.org/wiki/Parameterintegral#Leibnizregel_f.C3.BCr_Parameterintegrale

---

Danke für den Hinweis , ich hab das mal versucht .

So wie ich das sehe leitet man die Grenzen ab und Mulitpliziert diese Mit der Funktion die im Intervall steht nur das  man die eine variable die nicht in der Grenze vorgekommen ist mit der Grenze tauscht .

Ist die Ableitung für die Untere Grenze 0?

Und bei der Partiellen ableitung in dem Integrall dann ist da nur eine Gemeint also die nach omega?

Schaut das dann so aus ?

(1/k)*(1*f(t,t) -0*f(0,t) + (0 bis t)∫du*f(u)*cos(k(t-u))*k

---

Sieht richtig aus, wobei man das schwer lesen kann. Du weisst ja, was am Ende rauskommen muss. Wann immer Du auf was anderes kommst, dann weisst Du, dass Du Dich verrechnet hast.

PS: Der erste Teil vor dem Integral stimmt nicht.

---

meinst du die Definition hier  x(t):= dx(t)/dt .

das ist doch dieses Integral 1 mal ableiten oder? Ich meine ein Ergebnis steht nicht dabei oder was meinst du?

---

(1/k)*(1*f(t,t) -0*f(0,t) + (0 bis t)∫du*f(u)*cos(k(t-u))*k

Das ist falsch.

Ein Ergebnis für \(\dot{x}\) steht nicht in der Aufgabe, aber eines für \(\ddot{x}+k^2x\).

---

ah ok . kanst du mir zeigen wie du die erste ableitung gemacht hast? wäre nett !

---

Ich kann Dir die Regel runterkochen: $$\frac{d}{dt}\int_a^t g(t,u)\,du=\int_a^t g_t(t,u)\,du+g(t,t).$$ Bisschen was musst Du wohl noch selber machen. Es ist ja nun alles da.

---

ok das leuchtet mir schon ein bisschen ein ^^

ich habs nochmal probiert : g(t,t) kann ich nachvollziehen . steht das symbol gt im Integrall für die Partielle Ableitung der Funktion g (t,u) nach t ?

wenn ja dann komm ich da auf aud den gleichen faktor von vorher du*f(u)*cos(kt-ku)*k

was mache ich da falsch?

---

(1/k)*(1*f(t,t) -0*f(0,t) + (0 bis t)∫du*f(u)*cos(k(t-u))*k

Falsch ist, was Du vor's Integral gepinselt hattest.

---

Ich habs nochmal Probiert ^^

ich habe g(u,t) =f(u)*sin(kt -ku)

für u kommt die obere grenz Funktion rein die ist doch t . dann hatt man g(t,t) *1 ( Die Ableitung von t nach t)

das ist dann g(t,t)= f(t)*sin(kt-kt)=f(t)*0=0 ,

für die untere Grenze ergibt die ableitung nach t 0 weil konstante also fällt der Term auch weg.

kann das sein?

---

Es scheint ein guter Zeitpunkt gekommen, jetzt auch die zweite Ableitung noch auszurechnen, und dann zu schauen ob \(\ddot{x}+k^2x=f\) aufgeht.

---

waren die Faktoren vor dem Integral nun richtig das ich gleich weiter ableiten kann ?
Sozusagen muss ich "Fast" das Gleiche Integral nochmal ableiten sodass statt dem sinus nun ein cosinus drinnen ist .

Wenn ich das so mache wie vorher bekomme ich

(0 bis t)∫du*f(u)*(-1)sin(k(t-u))*k^2

Answer 1

Hi,
mit
$$ x(t) = \frac{1}{k} \int_0^t f(u) \sin[k(t-u)] du $$ folgt nach den in den Kommentaren angegebenen Regeln
$$ x'(t) = \frac{1}{k} \int_0^t f(u) \cos[k(t-u)] du \cdot k = \int_0^t f(u) \cos[k(t-u)] du  $$ und
$$ x''(t) = -k \int_0^t f(u) \sin[k(t-u)] du + f(t) $$ also
$$ x''(t) + k^2 x(t) = f(t) $$

Comments

Hallo ultim danke für deine Antwort .

Ich hab 2 fragen ;

1) Die Aussage folgt dann weil in der Dgl nach einsetzen für x (t) und x''(t) , steht f (t) = f(t) ?

2) warum sind die Anfangswerte gegeben wenn wir die gar nicht gebraucht haben ?

---

Hi, wenn Du $$ x(t) + k^2x''(t) $$ ausrechnest indem Du \( x(t) \) und das Ergebnis für \( x''(t) \) einsetzt kommt \( f(t) \) heraus und  das musstes Du zeigen. Die Anfangsbedingungen müssen auch noch nachgewiesen  werden.
$$ x(0) = \frac{1}{k} \int_0^0 f(u) \sin[k(0-u)] du = 0 $$ und
$$ x'(0) = \int_0^0 f(u) \cos[k(0-u)] du = 0 $$

---

Nur so Interesse halber ; Anfangsbedingungen für was braucht man die eigentlich bei Differentialgleichungen oder hier in den Beispiel, man hat sie zwar nachgewiesen das sie stimmen aber wofür ?

Ich danke dir vielmals !

---

Die Anfangsbedingungen machen Deine Lösung eindeutig. Hast Du keine, ergibt sich aus der DGL eine Lösung mit zwei freiwählbaren Parameter. Nimm z.B. die DGL

$$ x''(t) = g $$ dann folgt durch Integration $$ (1) \quad x'(t) = gt + k_1  $$ und dann $$ (2) \quad x(t) = g\frac{t^2}{2} +k_1t + k_2 $$

Aus z.B. \( x(0) = x'(0) = 0 \) folgt dann durch einsetzten von \( t = 0 \) in \( (1) \) und \( 2 \), dass \( k_1 = k_2 = 0 \) gelten muss. Also ist die Lösung

$$  x(t) = g\frac{t^2}{2} $$