Bestimme die spezielle Lösung der inhomogenen Differentialgleichung

Question

Hier habe den folgenden Ansatz genommen :

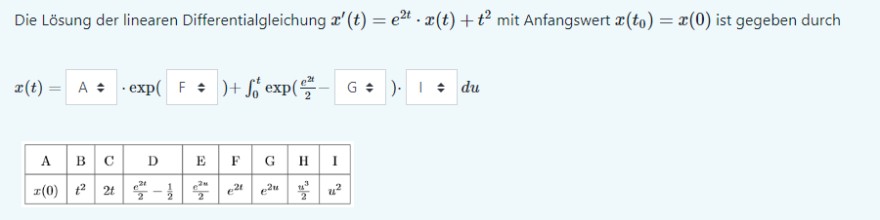
x' = f(t) * x + g(t)

Es handelt sich hier um eine inhomogene Differentialgleichung erster Ordnung nicht mit konstanten Koeffizienten wegen e^(2t), inhomogen wegen dem Störterm t^2.

Für die obige DGL habe ich zuerst die zugehörige homogene Lösung der DGL bestimmt, da komme ich auf xh = C*e^(∫f(t)*dt) und für irgendeine partikuläre Lösung der DGL komme ich auf xp = xh * ∫ (g(t)/xh)*dt, ich habe diese zuerst allgemein gelöst und dann habe ich die Summe also x = xh + xp gebildet und f(t) = e^(2t) und g(x) = t^2 mit der Anfangsbedingung in xh und xp eingesetzt und die spezielle Lösung der inhomogenen DGL bestimmt. Die einzelnen Kästchen habe ich dann in die leeren Felder zugeordnet.

Ich freue mich auf Antworten

Vielen Dank im Voraus

Comments

Ich komme zu einem anderen Ergebnis: Zunächst erhältst Du nicht x(0), wenn Du in Deiner Lösung t=0 setzt.

Im ersten exp-Term muss D statt F stehen...