Die Gerade g enthält die Punkte P(-3|-2) und Q(5|3).....Gib die Gleichung der Geraden g an.

Question

a) Gib die Gleichung der Geraden g an.
b) Wo schneidet g die Koordinatachsen?
c)Gib die Gleichung der zu g parallelen Geraden an, die durch den Koordinatenursprung geht.
d) Liegt der Punkt R(6|8) auf g?
e) Liegt der Punkt S(7|4,25) auf g?
Brauche hilfe... mit erklärung bitte

Comments

Damit du eine allfällige Antwort auch verstehst: Einige nützliche Formeln und Rechenbeschreibungen z.B. in folgendem 'Material zur Lektion'

https://www.matheretter.de/kurse/fkt/linear-nf

Answer 1

a)

P(-3|-2) und Q(5|3)

Steigung

m = (y1 - y2) / (x1 - x2) = (-2 - 3) / (-3 - 5) = -5 / -8 = 5/8

Punkt-Steigungs-Form

g(x) = m * (x - Px) + Py = 5/8 * (x - 5) + 3

b)

Schnittpunkt mit der Y-Achse

g(0) = 5/8 * (x - 5) + 3 = 5/8 * x - 1/8
Y-Achsenabschnitt bei (0, -1/8)

Nullstelle

g(x) = 0
5/8 * (x - 5) + 3 = 0
5/8 * (x - 5) = -3
x - 5 = -3 * 8 / 5
x = -3 * 8 / 5 + 5 = 1/5

c)

g(x) = 5/8 * (x - 5) + 3 = 5/8 * x - 1/8
g2(x) = 5/8 * x

d)

g(6) = 5/8 * 6 - 1/8 = 29/8 --> R liegt nicht auf g
g(7) = 5/8 * 7 - 1/8 = 4.25 --> S liegt auf g

Answer 2

Die Gerade g enthält die Punkte P(-3|-2) und Q(5|3).....gib die gleichung der geraden g an.
a) Gib die Gleichung der Geraden g an.

m = (Delta y) / (Delta x) = (3-(-2)) / (5-(-3)) = 5/8

Ansatz y = 5/8 x + q

Punkt einsetzen. 3 = 5/8 * 5 + q

3 - 25/8 = q

-1/8 = q

g: y = 5/8 x - 1/8

Kontrolle Graph:

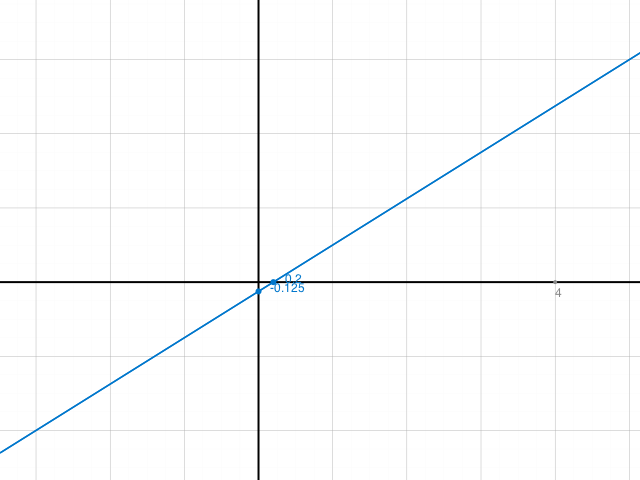
b) Wo schneidet g die Koordinatachsen?

x-Achse (y=0 einsetzen in  0 = 5/8 x - 1/8) bei x= 0.2, y-Achse (x=0 einsetzen in  y = 5/8 *0  - 1/8) bei y = -1/8

c)Gib die Gleichung der zu g parallelen Geraden an, die durch den Koordinatenursprung geht.

y = 5/8 x
d) Liegt der Punkt R(6|8) auf g?

Nein:  y = 5/8*6 - 1/8 = 30/8 - 1/8 = 29/8 = 8
e) Liegt der Punkt S(7|4,25) auf g?

 y = 5/8*7 - 1/8 = 35/8 - 1/8 = 34/8 = 17/4 = 4,25 stimmt. Also: ja