Steckbriefaufgabe: Parabeln 3. Ordnung mit:berührt die x-Achse in (0/0) und in P (-3/0) parallel zur Geraden y=6x

Question

Hilfeeeeeeeee, wie geht die Aufgabe?

1.Parabel 3.Ordnung

2.berührt  die x-Achse in (0/0)

3.in P (-3/0) parallel zur Geraden y=6x ? :/

Answer 1

1.Parabel 3.Ordnung

f(x) = ax^3 + bx^2 + cx + d
f'(x) = 3ax^2 + 2bx + c

2.berührt  die x-Achse in (0/0)

f(0) = 0
f'(0) = 0

3. in P (-3/0) parallel zur Geraden y = 6x ?

f(-3) = 0
f'(-3) = 6

Aus den Bedingungen erhält man folgende Gleichungen

d = 0
c = 0
-27a + 9b - 3c + d = 0
27a - 6b + c = 6

Die Lösung des Gleichungssystems ist a = 2/3, b = 2, c = 0 und d = 0

Hieraus erhält man die Funktionsgleichung:

f(x) = 2/3·x^3 + 2·x^2

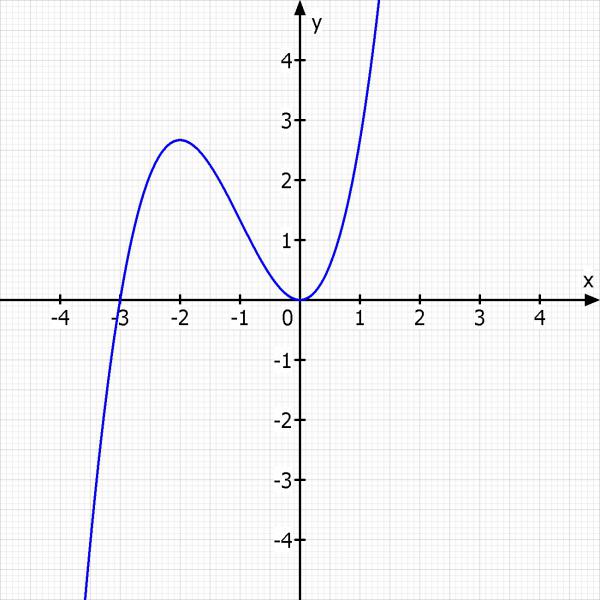
Ich mache noch eine Skizze

Comments

Aber warum sind c&d =0?

---

Weil du die Bedingungen 

f(0) = 0
a*0^3 + b*0^2 + c*0 + d = 0
d = 0

f'(0) = 0
3a*0^2 + 2b*0 + c = 0
c = 0

hast.

---

Achso jetzt habe ich das alles verstanden,vielen Dank :)

Answer 2

Text erkannt:

1. Parabel 3.Ordnung
2.berührt die \( x \)-Achse in \( (0 \mid 0) \)
3. \( \in P(-3 \mid 0) \) parallel zur Geraden \( y=6 x \)
\( f(x)=a \cdot x^{2} \cdot(x+3)=a \cdot x^{3}+3 a x^{2} \)
\( \frac{d f(x)}{d x}=3 a x^{2}+6 a x \)
\( \frac{d f(-3)}{d x}=3 a \cdot 9-6 a \cdot 3=9 a \rightarrow \rightarrow 9 a=6 \rightarrow \rightarrow a=\frac{2}{3} \)
\( f(x)=\frac{2}{3} \cdot x^{2} \cdot(x+3) \)