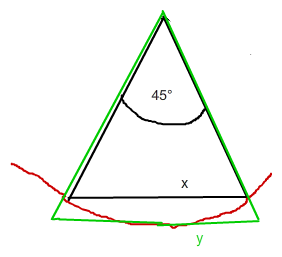
Wenn das rote die (verunglückte) Kreislinie ist und x die Seite des einbeschriebenen
8-ecks, dann ist 8*x < Kreisumfang < 8y bzw
8*x < 2*r*pi < 8yalso
4x / r < pi < 4y / r #
Also muss man x und y ausrechnen.
x ist die Basis in einem gleichschenkligen Dreieck mit Schenkel = r .
Da findest du bei Wikipedia
https://de.wikipedia.org/wiki/Achteck
(Kannst du aber auch leicht beweisen durch Teil eines dem Kreis einbeschriebenen
Quadrates.)
die Formel a = 2*ri *(√2 - 1) und hier ist ja a=x und ri = r also
x = 2*r *(√2 - 1) und damit für # 4x / r = 8 *(√2 - 1) ungefähr 3,31
Das wäre die untere Schranke für pi.
Außerdem gilt für die Höhe im schwarzen Dreieck h1^2 + (x/2 ^2 )= r^2
gibt für h1 = wurzel( 2*(√2 - 1) ) * r
Für y zeichne am besten mal die Höhe im grünen Dreieck ein und kannst dann
Strahlensatz anwenden h1 / r = (x/2) / (y/2) = x / y also
wurzel( 2*(√2 - 1) ) * r / r = x / y
also y = x / wurzel( 2*(√2 - 1) ) = 2*r *(√2 - 1) / wurzel( 2*(√2 - 1) )
gibt mit etwas Rechnerei y = r * wurzel( 2*(√2 - 1) also 4y / r ungefähr 3,64
als obere Schranke für pi.