Hallo ich solle das folgende Volumsintegral in zylinderkoordinaten berechnen :
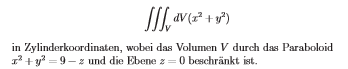
Wir haben aufgeschreiben zylinderkoordinaten sind
für x=ρ*cos(φ) , y=ρ*sin(φ) ,z=z
ergibt sich laut jakobi determinante für dV=ρ*dρ*dφ*dz
∫∫∫(x^2+y^2)dV= ∫∫∫(ρ^2*cos^2(φ)+ρ^2*sin^2(φ))ρ*dρ*dφ*dz=∫∫∫∫∫∫(ρ^3*dρ*dφ*dz
wenn ich das Integrieren will brauche ich die Grenzen aber ich verstehe das nicht ganz wie ich auf die komme , kann mir jemand helfen bitte .