Hallo,
die Menge \(B\) sei: $$B=\left\{ {\begin{pmatrix} r \cos(φ) \sin(θ)\\ r \sin(φ) \sin(θ)\\r \cos(θ) \end{pmatrix} ∈ R^3 \mid 0 ≤ r ≤ 1, \space 0 ≤ φ ≤ \frac\pi2,\space \frac\pi 2 ≤ θ ≤ π} \right\}$$mit der üblichen Definition von Kugelkoordinaten ist das in kartesischen Koordinaten:$$B=\left\{ {\begin{pmatrix}x\\ y\\ z \end{pmatrix} ∈ R^3 \mid x^2+y^2+z^2 ≤ 1, \space x \ge 0,\space y \ge 0, \space z \le 0} \right\}$$dies ist ein Achtel einer Kugel und sieht so aus:
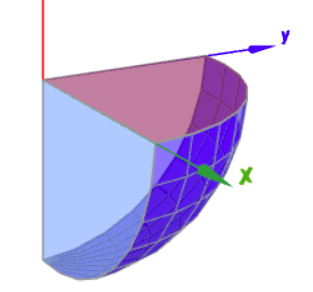
(klick auf das Bild, dann kannst Du es mit der Maus rotieren und bekommst einen besseren Eindruck)
$$C = \left\{(x, y, z) ∈ R^3 \mid x^2 + y^2 \le z^4,\space −2 \le z \le 3,\space x \ge 0 \right\}$$Zylinderkoordinaten sind i.A. definiert als$$x = r \cos \varphi\\ y = r \sin \varphi\\ z = h $$oben einsetzen gibt$$C = \left\{\begin{pmatrix} r \cos \varphi \\ r \sin \varphi\\ h \end{pmatrix} ∈ R^3 \mid r \ge 0, \space r \le h^2,\space −2 \le h \le 3,\space -\frac\pi 2 \le \varphi \le \frac\pi 2 \right\}$$und sieht so aus:
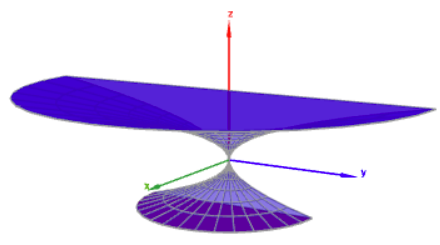
(klick drauf ...)
Gruß Werner