Trigonometrie. Frage zu speziellen Figuren .

Question

Hallo ich soll diese Figuren

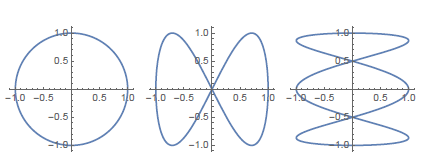
 a)als Wege der Kurven der Form t→(cos(nt),sin(mt)) darstellen .

Ich habe für das linkeste , t→(cos(nt),sin(mt)) =(1cos(1t),1sin(1t))=(cos(t),sin(t))

für das mittlere : habe ich wo gesehen das dass eine Lissajous Figur ist und gesehen dafür gibt es 2 Gleichungen ;

x=a1sin(b1t+c1) y=a2sin(b2t+c2) hier ist a1,a2 wohl 1 und dort steht das Phasenverhältniss Δφ=0 =c1-c2

und das Frequenzverhältniss :v=ω1/ω2=b1(b2=1/2 .

damit erhalte ich x=sin(t) und y=sin(2t) damit hat man X=(sin(t),sin(2t))=(cos(t)-π/2),sin(2t)) stimmt das soweit?

und das dritte weiß ich nicht so ganz .

und b)

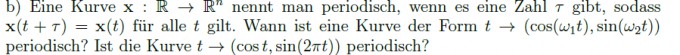
kann mir das jemand bitte erklären? danke !

Comments

Das sind Lissajous-Figuren: https://de.wikipedia.org/wiki/Lissajous-Figur

---

Danke Lu , das habe ich scon erkannt :)

Es verbleibt nur noch aufgabe b ) siehe Kommentare MC .

---

Hall oLiebe Community

habe eine e Frage

Zu punkt b Ich habe herausgefunden das wenn w1:w2 irrational ist ist Die Funktion nicht periodisch Jedo wie kann ich dies auch noch beweisen dass es immer stimmt

Schon einmal Danke im vorhinen

Answer 1

Diese 3 Bilder kann das Universal-Diagramm mit einem mal zeichnen:

http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm

Einfach Beispiel 11 bei x(t): cos(t) eintragen

und bei y(t) den globalen Parameter aB[0] von 1 bis 3 wandern lassen:

wenn man das letzte Bild um 90° drehen will, bedeutet das in Parameterdarstellung x und y vertauschen:

Hinweis: nur weil einige Menschen "Schreibfaul" sind, hat die um Pi/2 verschobene sin-Funktion einen eigenen Namen bekommen:

cos(x) = sin(x+Pi/2)

statt "vertauschen" funktioniert also auch "Argumente um Pi/2 verschieben"

Comments

Cool danke !

Dann würde ich folgende Ergebnisse haben:

1) f(t) = [cos(t), sin(t)]

2) f(t) = [cos(t), sin(2*t)]

3) f(t) = [sin(t),cos(3t)]=[cos(x+π/2),sin(3(t+π/2)]

---

zu b) da der Faktor für das Argument t eine irrationale Zahl ist, gibt es keine Wiederholung, d.h. wenn man lange genug zeichnet, wird jeder Punkt mal durchlaufen:

---

Dein 3) ist falsch, da der Faktor zum Argument entscheidend ist! Der Verhältnis-Faktor der x-Argumente muss 3 mal größer als die der y-Funktions-Argumente sein!

Habe das mal in einem Bild dargestellt. Um die Bilder nebeneinander zu bekommen habe ich mit einem x-Offset hinzugefügt (+aB[0]*2-4  ,das musst Du natürlich bei Deiner Aufgabe weglassen):

*((aB[0]<3)?aB[0]:1) bedeutet: solange aB[0] kleiner 3, Faktor=aB[0] ansonsten Faktor=1

*((aB[0]<3)?1:aB[0]) bedeutet: solange aB[0] kleiner 3, Faktor=1 ansonsten aB[0] {also 3}

---

Was ich mit Verschiebung sagen wollte: man kommt ohne die cos-Funktion aus. Alles nur sin-Kurven, die verschoben sind...

Im letzten Bild ersetze ich mal die cos um die verschobene sin, also:

cos(t*((aB[0]<3)?1:aB[0]))+aB[0]*2-4 = sin(t*((aB[0]<3)?1:aB[0])+PI/2)+aB[0]*2-4

---

Ah der 3 mal faktor verstehe , ich habe das Ergebnis vom MC noch mal getauscht obwohl es schon richtig ist .

Ok danke das kann ich so eingermaßen nachvollziehen .

Kanst du mir noch helfen wie ich zeigen kann , wann bei b) eine Kurve periodisch ist?

Mit x(t)=x(t+τ) .

---

Ich hatte es doch schon angedeutet und auch bei Wikipedia steht es :

periodisch, wenn Verhältnis ω₁/ω₂=N₁/N₂ rational (Bruch aus 2 ganzen Zahlen darstellbar).

Mit dem Plotter bedeutet das: eine Verschiebung von t_min und t_max ändert nichts am Bild!

Ob der Winkel t von 0...8 oder 1 ...9 oder 2 ... 10 läuft, ist egal.

Wenn aber Verhältnis eine irrationale Zahl (unendlich viele Nachkommastellen) ist, verschiebt sich das Bild ständig, da man nie die identischen Punkte wieder trifft (nicht periodisch):

Die Verschiebung von t wurde hier mit Addition des Argumentes realisiert: (t+aB[0]*11)

---

Ok alles klar danke !

Letze frage noch , damit ist das beispiel bei b) nicht periodisch weil ω1/ω2=1/2π kein Element aus ℚ ist ?

---

Ja, das hatten wir doch schon:

"...zu b) da der Faktor für das Argument t eine irrationale Zahl ist, gibt es keine Wiederholung..."

mit dem ausgemalten Bild

und

"...periodisch, wenn Verhältnis ω₁/ω₂=N₁/N₂ rational (Bruch aus 2 ganzen Zahlen darstellbar)...."

Answer 2

f(t) = [cos(t), sin(t)]

f(t) = [cos(t), sin(2*t)]

f(t) = [cos(3*t), sin(t)]

Comments

Hallo Mathecoach , wie komst du bei 2) und 3) auf den cosinus ?

Ist das nicht der sinus?

---

Das ist doch 1) nur abgeändert das die Schwingungsdauer bzw. Periodenlänge in x oder y Richtung verändert wird. Also bleibt eigentlich die Grundstruktur von 1) erhalten.

---

Ok danke das verstehe ich so einigermaßen .

Kanst du mir noch sagen wie man b erklärt?

---

Du sollst prüfen wann die Funktion x(t) = [cos(w1*t), sin(w2*t)] periodisch ist, d.h. wann gilt

x(t + r) = x(t)

---

Ah ok , ist das so gemeint das der Endpunkt gleich dem Anfangspunkt ist sodass sich da eine geschlossene sich immer wiederholenede kurve ergibt?

Wenn ja , wahrscheinlich dann für alle rationalen Vielfachen von π ?

---

Ja. Das würde ich auch vermuten. Kannst du das auch zeigen?

---

Hmm ich dachte zum anfagen kann man das so aufschreiben :

x(t+τ)-x(t)=0 . ⇒x(cos(w1t(t+τ),sin(w2t(t+τ)) -(cos(w1t),sin(w2t))

villeicht mit den Addionstheormen weitermachen , oder denke ich da zu kompliziert?