Induktionsbeweis - konvexe Menge

Question

Ich habe hier eine interessante Aufgabe:

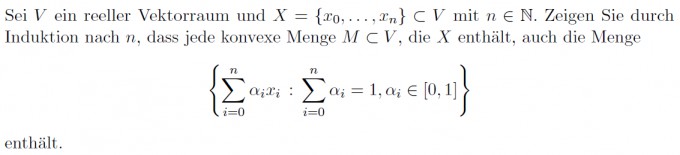
Eigenschaft einer konvexen Menge war ja:

$$ \lambda a+(1-\lambda)b\in M $$ mit $$ a,b\in M, \lambda \in R, 0\leq\lambda\leq1 $$

Das Problem ist, dass ich keinen richtigen Ansatz für den Induktionsschritt habe. 

$$ \sum _{ i=0 }^{ n+1 }{ a_ix_i } =\sum _{ i=0 }^{ n }{ a_ix_i } + a_{n+1}x_{n+1} $$

Wie zeige ich letztlich, dass diese Menge wieder in M enthalten ist?

Answer 1

Wähle \( \lambda \) so, dass \( a_{n+1} = 1-\lambda \) ist.

Dann genügt es zu zeigen, dass \( \sum _{ i=0 }^{ n }{ a_ix_i } = \lambda a \) für ein \( a\in M \) ist.

Ein solches \( a\in M \) existiert, weil  \( \sum_{i=0}^n\frac{a_i}{1-a_{n+1}} = 1 \) und \( 0\leq \frac{a_i}{1-a_{n+1}}\leq 1\ \forall i\in \{0,\dots,n\} \) ist.