wir haben eine Matrix B gegeben 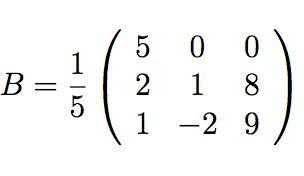
Wir sollen dazu die Jordanform bestimmen und die Transformationsmatrizen sodass T^-1 B T = J ergibt.
Ich habe schon den Eigenwert 1 mit algebraischer Vielfachheit 3 ausgerechnet un den Eigenraum E_B(1) = span{(2,1,0)^T ; (-4,0,1)^T}. Jetzt brauche ich ja noch einen dritten Vektor um meine Transformationsmatrix angeben zu können. Ich weiß aber nicht wie ich in diesem Fall das machen soll, da ich ja das entstehende LGS (B-\lambdaE)v mit meinen beiden Eigenvektoren so nicht lösbar ist (erste Zeile der Matrix ist 0, erste Zeile der Eigenvektoren sind ungleich 0)
Danke