Wie berechnet man hier den Winkel alpha? Winkelberechnung

Question

Wie berechnet man hier den Winkel alpha? Es gibt keine Angabe außer die 90° Winkel und den Winkelsummensatz im Dreieck von 180°.

Comments

Sind die beiden Kreisen gleich groß?

---

Ja die Kreise sind gleich groß.

---

Aus der Skizze wird ersichtlich das beide Kreise denselben
Radius r haben.
Der Abstand zwischen den Schnittstellen / Mittelpunkten
der beiden Kreise ist r.

@Fragesteller
Es gibt keine Angabe außer die 90° Winkel
wo ist der rechter Winkel ?

---

Die 90° Winkel sind anscheinend an den beiden weißen kreisen.

---

Wie löst man diese Aufgabe?Die Kreise sind gleich groß und es scheint so, als ob an den zwei weißen Punkten die Winkel 90° betragen.

---

Garantiert nicht.

Wemm dem so wäre dann müßte sich eine Symmtrische Figur zu
linkem Eckpunkt  - mittlerer Kreuzungspunkt - rechter Schnittpunkt der Kreise
ergeben. Dies müßte eine Gerade sein.
Wie man sieht ist es keine Gerade.

Hast du den Orginalfragetext.

---

Nein dazu gab es keinen....

---

Das einzige was sich folgern läßt.
Die 3 rot markierten Strecken sind gleich lang.
Radius der Kreise

---

Das einzige was sich folgern läßt

Das muss ja Unsinn sein, denn wie sollte man dann auf die Lösung  α = 60°  kommen ?

---

Hier meine Zeichnungen, aber noch keine Rechnung.

und dann

zum Schluss 

Answer 1

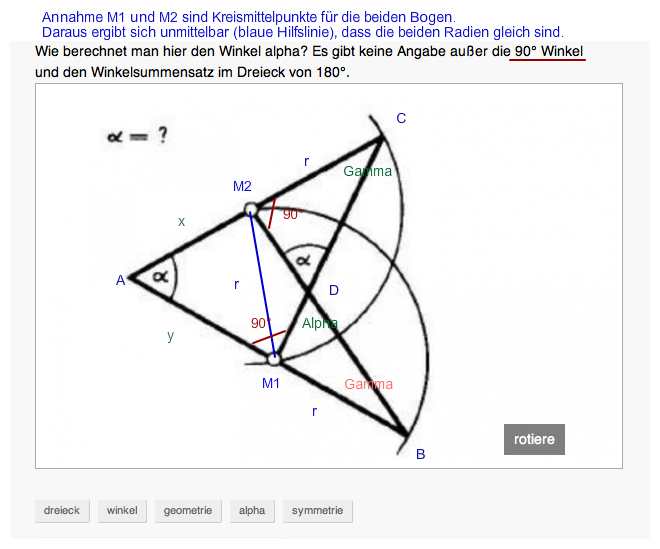
Da ABM2 und ACM1 die gleichen Winkel haben. (vgl. meine Zeichnungen im Kommentar), muss gelten

x /(y+r) = y /(x+r)   = cos (alpha)  wobei x,y und r>0. 

Gleichung stimmt auf jeden Fall für x = y. Weitere Möglichkeiten? 

x(x+r) = y(y+r) 

x^2 + xr = y^2 + yr

y^2 + yr - (x^2 +xr) = 0

y_(1,2) = 1/2 ( -r ± √( r^2 + 4(x^2 + xr)) 

= 1/2 (-r ± √(r^2 + 4xr + (2x)^2) 

= 1/2 (-r ± √(r + 2x)^2) 

= 1/2 (-r ± (r+2x)) 

y_(1) =1/2 * 2x = x                

y_(1) = 1/2 *(-2r - 2x) = -r-x        neg. geometrisch nicht möglich.

Nun weisst du also schon mal, dass x = y. 

Hast du inzwischen schon erfahren, wie man z.B. x=r noch zeigen könnte? 

Oder kennst du einen eleganteren Weg?