Gebrochenrationale Funktion und Graphik f(x) = (-x^3 + 2x^2 + 4x - 8)/(x^2 -1)

Question

Hallo. Kann jemand mir helfen ? Schönen Dank

Answer 1

1)

wenn du im Zähler die Nullstelle x=2 durch Probieren gefunden hast, machst du die Polynomdivision

(- x² + 2·x² + 4·x - 8) : (x-2) = 4 -x² = - (x-2) • (x+2)

also :  f(x) = \(\frac{- (x-2)^2· (x+2)}{(x-1)·(x+1)}\) 

Du hast also Nullstellen bei x = 2 (doppelt → Extremstelle)  und x = -2

und Polstellen mit Vorzeichenwechsel bei  x = 1 und x = -1 

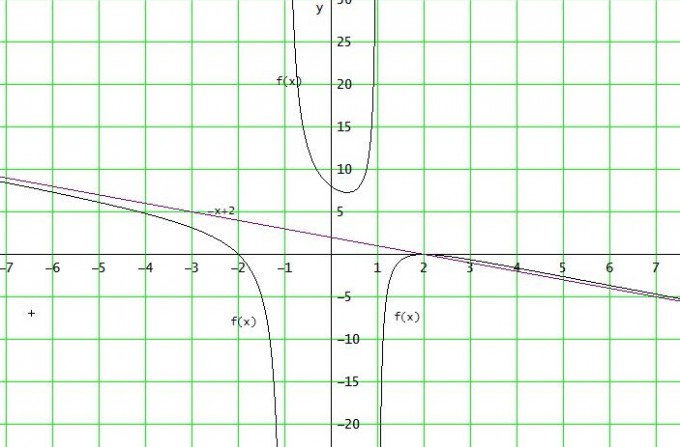
Wenn man jetzt noch die Asymptotenfunktion berechnet, hat man schon einen guten Überblick über den Graph:

(- x³ + 2·x² + 4·x - 8) : (x² -1) = -x + 2 + (3x - 6)/(x² - 1)

Asymtotenfunktion : f_A(x) = -x + 2

hier  findest du einen Rechner für die Polynomdivision

2)

Edit: Faktor (x+2) nach Kommentarvon Georg im Zähler eingefügt:

f(x) = \(\frac{x·(x-2)·(x+2)·(x+5)}{(x-1)·(x+1)·(x+5)·(x-6)^2}\)  

Nullstellen: x=0, x=±2  weil die Linearfaktoren im Nenner nicht vorkommem

Lücke: x=-5  weil sich der LF im Nenner komplett wegkürzen lässt

Polstelle ohne VZW:  x=-6  weil der LF im Nenner in gerader Potenz steht

Polstellen mit VZW:  x=±1   weil die Linearfaktoren im Nenner in ungerader Potenz stehen

Gruß Wolfgang

Comments

Hallo Wolfgang,

bei 2.) hast du bei Nullstellen x = -2 vergessen. Der Term ( x + 2 )
wäre noch einzufügen.

Wie immer lieb gemeint.

mfg Georg

---

Hallo Georg,

Stimmt, im Zähler fehlt der Faktor (x+2). Danke für den Hinweis, werde es korrigieren.

Gruß Wolfgang

---

Ach so. Jetzt habe ich versatnden. Aber auf der Graphik können Sie noch ein bisschen noch klar machen ? 

---

die genaue Lage des Tiefpunkts ergibt sich nur, wenn man mit der 1. Ableitung arbeitet.

Er muss aber wegen fehlender Nullstellen zwischen x=-1 und x=1 und dem Verhalten an den Polstellen (mit VZW) über der x-Achse liegen:

geht x von links an 1 (bzw. von rechts an -1) heran, streben die Funktionswerte jeweils gegen ∞

Answer 2

So würde ich die Funktion konstruieren. Schritt für Schritt.

Hier zur Kontrolle der Graph

Bin bei Bedarf gern weiter behilflich.

Comments

Können Sie mir die Graphik Nummer 1 erklären ? 

---

Einfache Nullstellen im Nenner (=unten) , die sich nicht kürzen lassen, bedeuten Vorzeichenwechsel. 

Grund: Vorzeichenwechsel ja oder nein funktioniert wie bei der Vielfachheit von Nullstellen von Polynomen.

---

Hallo Fedrixsakbes,

es muß eine sogenannte Kurvendiskussion durchgeführt werden.

Definitionsbereich, Polstellen, Verhalten der Funktion an den Rändern
und Polstellen, Nullstellen, Extrempunkte, Asymptoten.

Dann kann gezeichnet werden

Wolfgang hat dies gemacht,

Ich kann das aber auch nocheinmal machen.  Ableitungen / Extremstellen
sagt dir etwas ?

Ansonsten müßtest du deine Frage noch einmal besser konkretisieren.

mfg Georg

---

Die Kurvendiskussion können wir dann schrittweise aufbauen.