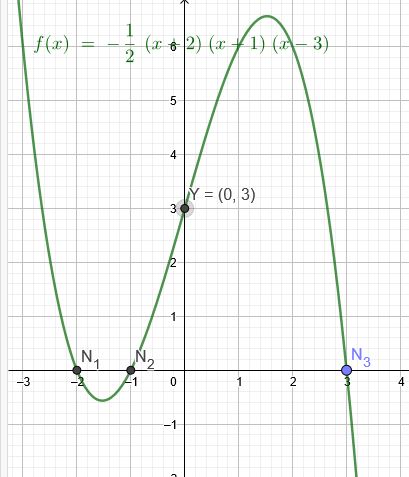
3a)
Ich wähle die Nullstellenform der kubischen Parabel:
\(f(x)=a(x-N_1)(x-N_2)(x-N_3)\)
\(f(x)=a(x+2)(x+1)(x-3)\)
Der Graph schneidet die y-Achse in \(Y(0|3)\):
\(f(0)=a(0+2)(0+1)(0-3)=-6a=3\)
\(a=- \frac{1}{2} \)
\(f(x)=- \frac{1}{2}(x+2)(x+1)(x-3)\)
3b)
Verlauf Graphenverlauf beschreiben. Möglichkeit über Wertetabelle oder Funktionsplotter (eventuell GeoGebra).
\(f_1(x)=\frac{1}{3}x^3-\frac{7}{2}x-3\)
\(f_1(0)=-3\)
\(Y_1(0|-3)\):
Beide Funktionen sind Parabeln 3.Ordnung.
Das Spiegelbild von \(Y_1(0|3)\) bezüglich der x-Achse ist \(Y_2(0|-3)\).
Beide Graphen sind punktsymmetrisch zum Wendepunkt.
3c) Bestimmung der Geraden \(h(x)\)
\(f_1(0)=-3\) \(Y_1(0|-3)\)
\(f_1(5)=\frac{1}{3}\cdot 5^3-\frac{7}{2}\cdot 5-3=\frac{127}{6}\)
\(S(5|\frac{127}{6})\)
2 Punkteform der Geraden:
\( \frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1} \)
\( \frac{\frac{127}{6}+3}{5-0}=\frac{y+3}{x-0} \)
\(y= \frac{29}{6}x-3 \)
Finde Begründung für einen weiteren Schnittpunkt.
Berechne diesen.
d) Das kannst du selbst.