Quadratische Betragsungleichung mit 2 Beträgen - Lösungsmenge

Question

ich komme mit dieser Aufgabe nicht klar:

|x²-2| ≤ |4x|

Ich habe einfach versucht Fälle aufzustellen und habe jetzt im

1. und 2. Fall x1=5 und x2=-1 und

im 3. Fallx1=1 und x2=-5 raus.

Ist das erstmal richtig? Wie komme ich nun zur Lösungsmenge?

Danke.

Comments

Nur so viel: Die Lösung ist nicht richtig. Lösungsmenge sind die Zahlen zwischen -√6- 2 und 2-√6 sowie zwischen √6 - 2 und √6+2.

Answer 1

 

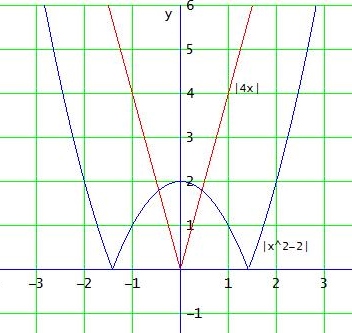
der Term 4x hat die Nullstelle x=0,  x² - 1  die Nullstellen x = ±√2

In den Intervallen ] -∞ ; - √2 [ , ] -√2 ; 0 [ , ] 0 ; √2 [ und ] √2 ; ∞ [ haben beide Terme in den Beträgen konstantes Vorzeichen:

                    ] -∞ ; - √2 [        ] -√2 ; 0 [        ] 0 ; √2 [      ] √2 ; ∞ [ 

4x                       -                       -                     +                   +

x² - 2                 +                       -                     -                   +

Bei positivem  Vorzeichen kann man die Betragstriche einfach weglassen, bei  -  muss man ein Minuszeichen vor den geklammerten Term setzen.

Damit erhältst du 4 Fälle mit 4 quadratische Ungleichungen ( bei den Nullstellen selbst ist es gleichgültig, in welchen der angrenzenden Fälle du sie übernimmst). Die 4 Teillösungsmengen musst du du zur Gesamtlösungsmenge vereinigen.

x ≤ -√2 :           -4x ≤  x² - 2

-√2 < x ≤ 0 :      -4x ≤ -x² + 2

0 < x ≤ √2 :       4x ≤ -x² + 2

x > √2 :              4x ≤  x² - 2

Zur Kontrolle:   L =  [- √6 - 2 ; 2 - √6 ]  ∪ [ √6 - 2 ; √6 + 2 ]

Gruß Wolfgang

Answer 2

| x²-2| ≤ |4x|    

x²-2 ist negativ im Bereich von ] - √2  ;  √2 [

und 4x ändert das VZ bei x=0 .

Also würde ich folgende Fälle betrachten:

1. Fall   x < - √2     da ist  | x²-2| =   x²-2   und     |4x|    =  -4x

also bleibt zu untersuchen       x²-2 ≤ 4x  

                                         x²  -4x -2 ≤ 0 

                                          x²  -4x +4   ≤ 6 

                                            ( x-2) ^2 ≤ 6  

                                x-2 ≥ √6    oder   x-2 ≤ -√6  

                                     x ≥ 2 +√6   oder  x ≤ 2 - √6  

Für den Fall   x < - √2   gilt die Ungl. also immer, da  - √2   <  2 - √6  

2. Fall  - √2   ≤ x ≤ 0    entsprechend.....

Answer 3

|x²-2| ≤ |4x|

Da links und rechts etwas positives steht stimmt auch

( x^2 - 2) ^2 ≤ (4x)^2

x^4 - 4x^2 + 4 ≤ 16 x^2
x^4 - 20 x^2 ≤ -4

Ersetzen
z = x^2

z^2 - 20 * z ≤ -4
z^2 - 20 * z + 10^2 ≤ -4  + 100
( z - 10)^2 ≤ 96
-√ 96 ≤ z - 10 ≤ √ 96   | + 10
-9.8 + 10 ≤ z ≤  9.8 + 10
0.2 ≤ z ≤ 19.8

Rückersetzen
0.2 ≤ x^2 ≤ 19.8

x^2 ≥ 0.2

x ≥ √ 0.2
x ≥ 0.45
und
x ≤ - √ 0.2
x ≤ -0.45

x^2 ≤  19.8
- √ 19.8 ≤ x ≤ √ 19.8

- 4.45 ≤ x ≤ 4.45

Die Zahlenbereiche

Die Schnittmenge wäre

-4.45 bis -0.45  und 0.45 bis 4.45

Die Gleichung

|x²-2| ≤ |4x|

wurde umgeformt zu

0 ≤ |4x| - |x²-2|

Alles was oberhalb der x-Achse ist gehört zur Löungsmenge