ich muss beweisen, dass es keinen Satz φ in FO{E} gibt mit:
G |= φ ⇐⇒ G ist ein planarer (ungerichteter) Graph
Hinweis: Betrachten Sie den folgenden planaren Multi-Graphen2 G und den nicht-planeren Graphen H: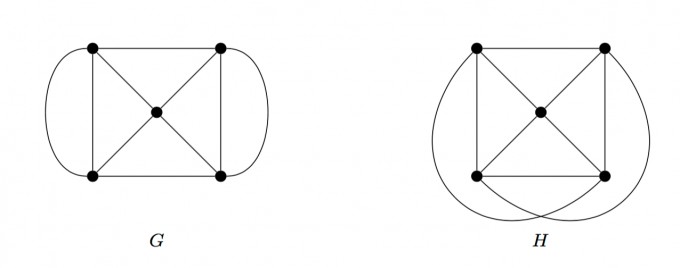
Konstruieren Sie nun zwei Familien (Gn)n∈N und (Hn)n∈N von planaren bzw. nicht-planaren ungerichteten Graphen (keine Multi-Graphen!) und verwenden Sie dann die Methode von Eh- renfeucht und Fraïssé. Es genügt, die Gewinnstrategien der Duplikatorin in den entsprechenden Ehrenfeucht-Fraïssé-Spielen nur zu skizzieren.
Könnte jemand mir dabei helfen. Mein Problem liegt daran, dass ich nicht genau weiss, wie man eine Familie von Graphen ausdrucken kann.
Danke.