ich will auch mal eine Berechnung versuchen. Es kommt darauf an wie der
Bewegungsablauf gedeutet wird.
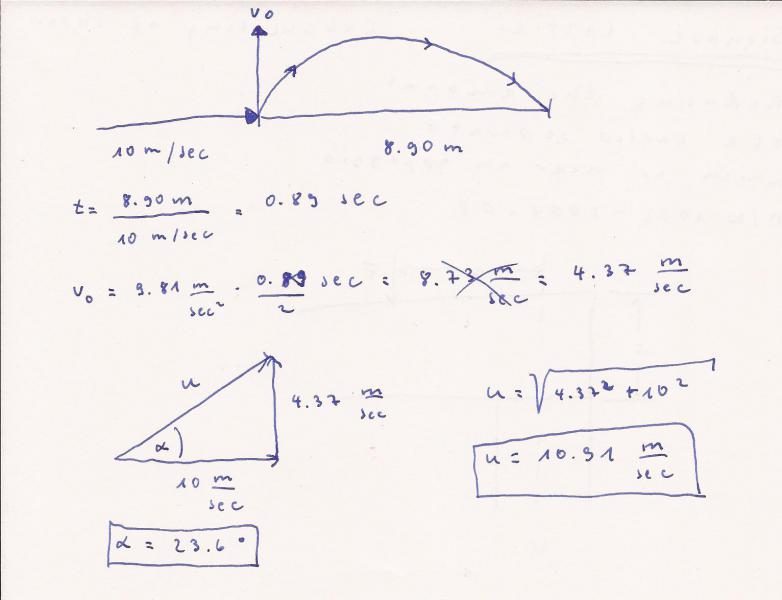
Bob Beamom springt mit 10 m/sec Horizontalgeschwindigkeit eine Strecke von
8.90 m und ist somit 0.89 sec in der Luft.
Beim Absprung drückt er sich zusätzlich nach oben ab. Diese Geschwindigkeit
erreicht er nachdem der Fuß den Erdboden verlassen hat. Diese vertikale Ge-
schwindigkeit reduziert sich zum Scheitelpunkt auf null. Mit derselben Ge-
schwindikeit kommt er auch wieder auf.
v(o) = 0.89 sec / 2 * 9.81 m/sec^2 = 4.37 m/sec.
u ist die zusammengesetzte Geschwindigkeit horizontal und vertikal und kann
mit dem Pythagoras zu 10.91 m/sec berechnet werden:
Der Winkel alpha beträgt 23.6 °.
Ich kann momentan keinen Fehler bei mir erkennen. Mich irritiert der Winkel von
23.6 ° allerdings. Die größte Weite beim schrägen Wurf wird bei 45 ° erzielt.
mfg Georg
mfg