Hallo die Aufgabe lautet :
Welche Beziehungen mussen zwischen α,β,γ und δ gelten, damit das Glei-
chungssystem mit der folgenden erweiterten Matrix mindestens eine Lösung besitzt?
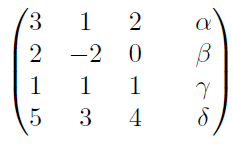
ich hab mir überlegt einfach das Gauß -Verfahren anzuwenden und zu schauen was passiert .
Wenn ich in der ersten Zeile 3 als PVE wähle und dann II- 2/3*I , III-1/3*I , und IIII-5/3*I rechne ergibt sich in den letzen 2 zeilen die gleichen Koeffizienten(unerweiter , also ohne lösunggspalte ) indem man dann zb eine von der anderen abzieht ergibt sich eine 0-Zeile . die Lösungsseite der 0 zeile ist jedoch nicht 0 . da steht zb noch in der in der letzten zeile δ-5/3*α=0 => δ=5/3α .
die 5/3 waren aber genau der Multiplikator den ich gewählt habe um die 4-Zeile zu bearbeiten.
weiters habe ich daraus geschlossen dass die Zeile der Form :0....0=a≠0 ein Widerspruch in sich ist und somit würde das Gleichungssystem hier keine Lösung haben .
Im allgemeinen Fällt mir dazu ein wenn sich 0-Zeilen ergeben muss a=0 sein und dass passiert hier nur wenn zb.δ=5/3α .
was sagt ihr dazu ?