Beschreibende Statistik - Fairer Münze und Fairer Würfel - Brauche dringen eure Hilfe!

Question

Zweistufiges Experiment: Fairer Wüfel wird einmal geworfen, dann werden so viele Münzwürfe mit einer ebenfalls fairen Münze durchgeführt, wie die Augenzahl des Würfels ergab, aber höchstens drei Würfe.

a. Stellen sie diese Experiment durch einen geeigneten Wahrscheinlichkeitsbaum dar und geben sie für alle möglichen Ergebnisse bzw. Abläufe deren Wahrscheinlichkeiten an.

b. Mit welcher WSK erhält man dann insgesamt genau zweimal Kopf?

c. Mit welcher WSK erhält man nach einem Sechserwurf genau zweimal Kopf?

d. Mit welcher WSK wird die Münze genau zweimal geworfen und ergibt zweimal Kopf?

Answer 1

Bei mir w=Wappen=Kopf

An dem Baum fehlen noch ganz viele Wahrscheinlichkeiten mit 1/2 .

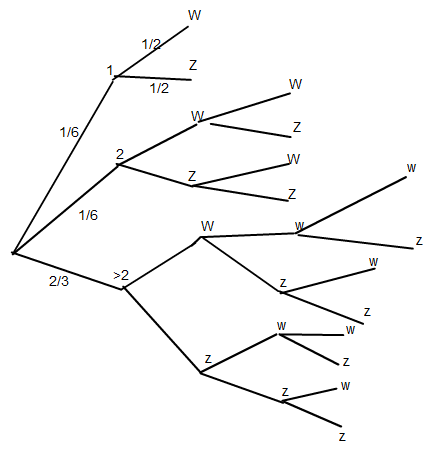
Im einzelnen sind die Ergebnisse

p( 1;w) =  1/6 * 1/2 = 1/12

p( 1;z) =  1/6 * 1/2 = 1/12

p(2;ww) = 1/6 * 1/2 * 1/2 = 1/24

p(2;wz) = 1/6 * 1/2 * 1/2 = 1/24

p(2;zw) = 1/6 * 1/2 * 1/2 = 1/24

p(2;zz) = 1/6 * 1/2 * 1/2 = 1/24

p( >2;zzz)=2/3*1/2*1/2*1/2 = 1/12

etc.

b) p(2;ww ) + p(>2;wwz)+p(>2;wzw)+p(>2;zww)

= 1/12 + 1/12 + 1/12 + 1/12 = 1/3

c) p(6;wwz)+p(6;wzw)+p(6zww)

= 1/6*1/2*1/2*1/2 + 1/6*1/2*1/2*1/2 +1/6*1/2*1/2*1/2

= 1/16

Comments

Vielen Dank für die schnelle Antwort!!!!

---

eine Frage hätte ich noch....wieso starte ich beim Baum mit 1/6, 1/6 und 2/3 ? Ich dachte das ich wahrscheinlich oben mit 6 Ästen beginnen muss und dann jeweils zwei Äste mit Kopf und Zahl zeichnen muss.

---

Das kannst du machen, aber dann wird der Baum doch sehr groß. 

Da höchstens 3-mal die Münze geworfen wird, habe ich die

4 Äste für 3456 einfach zusammengefasst, und dann natürlich

die Wahrscheinlichkeit 4/6 bzw. 2/3.

---

aaah ok, danke...hab mir das schon gedacht...aber safety first! DANKE!!