Teilerfunktion (fast) ohne Formeln

Question

In der Wikipedia habe ich die Teilerfunktion nachgeschlagen, aber wegen der Formeln nicht verstanden. Geht es verständlicher? Was lässt sich über ihre Bedeutung sagen?

Comments

Gib mal den Link an und was genau dein Problem ist.

Answer 1

Vielleicht reicht ja ein Beispiel:

Es ist lt. Wikipedia  σ_k(n) = Summe über alle Teiler d von n und aufaddiert wird d^k  .

Das wäre etwa für 

σ₂(6)  =  1^2 + 2^2 + 3^2 + 6^2  = 1  + 4  + 9  +36 = 50

weil nämlich 1 , 2 , 3 und 6 die einzigen Teiler von 6 sind und

wegen k = 2 werden sie jeweils quadriert.  Oder auch

σ₁(8)  =  1^1 + 2^1 + 4^1 + 8^1  =  1+2+4+8 = 15 .

Comments

Das Beispiel hat mir auf die Sprünge geholfen, so dass nun auch ich mit der Teilerfunktion wenigstens etwas anfangen kann.

Demnach ist "Teilerfunktion" ein kürzeres Wort für "Teilerpotenzsummenfunktion", stimmt's?

PS. Ist dieser Kommentar jetzt mehrmals angekommen? Ich hatte nämlich noch die E-Mail-Bestätigung nachzuholen, um die Antwort bewerten zu können.

---

Demnach ist "Teilerfunktion" ein kürzeres Wort für "Teilerpotenzsummenfunktion", stimmt's?

Ist wohl so, ich kannte nur das lange Wort.

PS. Ist dieser Kommentar jetzt mehrmals angekommen? Ich hatte nämlich noch die E-Mail-Bestätigung nachzuholen, um die Antwort bewerten zu können.

Alles OK.

Answer 2

Die Teilerfunktion hat 2 Parameter und wird auch divisorsigma(x,y) genannt {z.B. WolframAlpha}

Interessant ist vor allem der Spezialfall x=0 also die

Teileranzahlfunktion: divisorsigma(0,i)

sie gibt die Anzahl der Teiler an, die eine Zahl i hat. Jede Primzahl hat nur 2 Teiler (sich selbst und 1), also:

if divisorsigma(0,i) ==2 -> dann ist i Primzahl

Der Iterationsrechner rechnet das im Beispiel 131 online vor:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#ZZZZZ0131

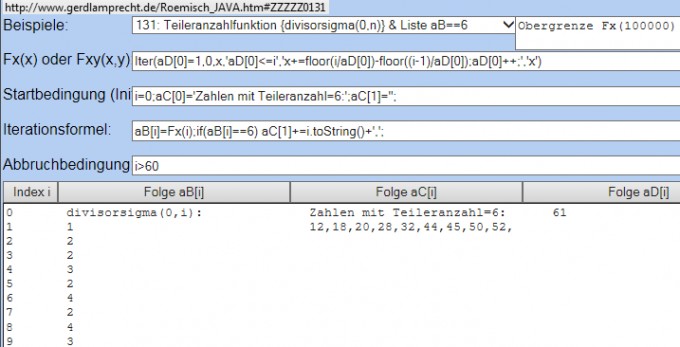
wobei floor(x) nichts weiter als Abrunden bis zur ganzen Zahl bedeutet.

aD[0] ist einfach nur eine Hilfsvariable, die bei 1 beginnt und mit aD[0]++ 

pro Schritt um 1 addiert wird. In der internen Variable x+=... werden also nur Brüche aus gerundeten Unterbrüchen aufsummiert -> und das Egebnis der Funktion Fx(x) an die Feldvariable aB[i] übergeben, was unten die TabellenSpalte mit den Zeilen (Index) ab i=1 ergibt.

Zusätzlich werden hier noch in aC[1] die Zahlen {bis 60} gesammelt, die alle genau 6 Teiler besitzen.

Natürlich kann man die Abbruchbedingung vergrößern und bekommt so mehr Ergebnisse.