Definition des Arkustangens

Question

in der Vorlesung haben wir gelernt, dass der Tangens definiert ist als tan(x)= sin(x)/cos(x).

Ich soll nun anhand des Tangens, die Umkehrfunktion, also den Arkustangens definieren.

Ich habe versucht den Quotienten sin(x)/cos(x) komplex darzustellen und dann nach dem x umzustellen, komme dabei aber nicht sehr weit. Kann mir jemand einen Tipp geben wie ich den Arkustangens am besten über den Tangens definiere?

Answer 1

tan: ℝ → ℝ , x ↦ tan(x) hat keine Umkehrfunktion, weil f nicht injektiv ist (weil es verschiedene x-Werte gibt, die den gleichen Funktionswert haben.

Wenn man aber den Definitionsbereich passend einschränkt, dann ist

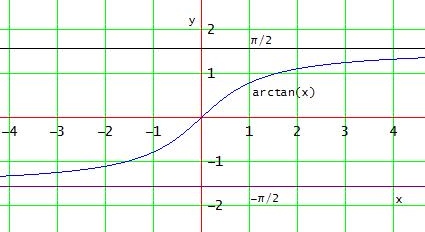
f: ] -π/2 ; π/2 [  → ℝ , x ↦ tan(x) injektiv und besitzt die Umkehrfunktion

f^-1: ℝ → ] -π/2 ; π/2 [  ;  x  ↦ arctan(x)

[ der Name arctan wird dieser Umkehrfunktion einfach per Definition zugeornet (ähnlich wie man ln als Umkehrfunktion der Exponentialfunktion definiert) ]

https://de.wikipedia.org/wiki/Arkustangens_und_Arkuskotangens

> Ich soll nun anhand des Tangens, die Umkehrfunktion, also den Arkustangens definieren.

Da der Graph einer Umkehrfunktion sich aus dem der Funktion durch Spiegelung an der 1. Winkelhalbierenden ( = Vertauschung von x-  und y-Werten)  ergibt, erfüllt man diese Forderung wohl am ehesten mit der Beschreibung

arctan ist die Funktion, deren Graph die Punktmenge 

{ ( tan(x) | x ) |  x ∈  ] -π/2 ; π/2 [  }  darstellt.

Gruß Wolfgang