ich habe ein kleines Problem beim bilden einer Linearkombination von 2 Eigenvektoren. Also ich soll aus einer Matrix A alle Eigenvektoren sowie verallgemeinerte Eigenvektoren bestimmen zu einer Basis der R^3 .
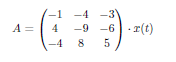
Der dreifache Eigenwert ist -1. Und die dann hab ich noch EV1=(2|1|0) ; EV2=(3|0|2)
Als Bemerkung gab es noch :
Ich habe schon nach geschaut wie ich eine Linerakombination zu verstehen habe , nur ich verstehe nicht wie ich damit auf den verallgemeinerten EV kommen soll.
Danke schinmal im Voraus
