Quadratische Gleichung: Mast mit einem Knick

Question

liebe Mathematiker!

Ich beschäftige mich während der Ferien mit Mathe und wurde bei einem Test von der folgenden Frage getroffen:

Ein 10m hoher Mast wurde vom Sturm geknickt. Die Spitze berührt den Erdboden 5m vom Fußpunkt des Mastes entfernt. In welcher Höhe befindet sich die Knickstelle?

Die folgende Gleichung ist gegeben:

                                  x²+5²=(10−x)²

1. Löse die Aufgabe, indem du

a) beschreibst, wie Anna auf die Gleichung gekommen ist,

b) die Gleichung löst und

c) die Antwort formulierst.

2. Löse anschließend die Aufgabe in der folgenden allgemeineren Form: Ein Mast der Höhe h wurde vom Sturm geknickt. die Spitze berührt den Erdboden in der Entfernung w vom Fußpunkt des Mastes. In welcher Höhe befindet sich die Knickstelle?
Gehe dabei darauf ein, welche Bedingungen für h und w gelten müssen, damit die Aufgabe sinnvoll ist.

Lösung:

Ich habe nur die Antwort für b) (3.75m), bin aber selbst nicht sicher, was genau dieser Schnittpunkt bedeutet - x-Stelle für den Knick?
Ich habe mehrmals versucht, die anderen Aufgaben erfolgreich zu beenden - jedoch erfolglos. 
Ich kann nicht verstehen, warum genau diese zwei Funktionen benutzt werden. (10-x)² sieht etwa logischer für mich aus, aber der Schnittpunkt mit der anderen - was ist hier gemeint?

Ich brauche ein paar Anweisungen. 

 

Comments

Das Wort Schnittpunkt hast allein Du benutzt, die Aufgabe erwähnt es nicht...

Answer 1

Hi,

ich denke eine Zeichnung beantwortet schon fast alle Fragen:

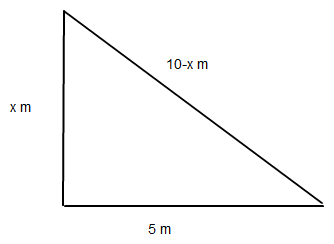
(Die 10-x kommen daher, dass der Mast aus der Länge x und der Hypotenuse bestehen. Da der Mast 10 m lang ist, muss die Hypotenuse 10-x m lang sein)

a) Das ist also direkt der Pythagoras.

b) Ja, da hast Du wohl richtig gerechnet: x=3,75

c) Wie aus der Skizze ersichtlich und aus der Rechnung bekannt, ist der Mast bei einer Höhe von 3,75 m umgeknickt.

 

2. Das nun noch allgemein. Statt 10-x wähle h-x für die Hypotenuse, die Entfernung der Spitze ist nicht 5 m, sondern w m.:

x²+w²=(h−x)²

x^2+w^2=h^2-2hx+x^2  |-x^2

w^2=h^2-2hx    |-h^2

w^2-h^2=-2hx   |:(-2h)

x=(h^2-w^2)/2h

 

Für w und h muss gelten, dass sie >0 sind (d.h. für die obige Gleichung ist explizit h≠0 gefordert, und aus logischen Gründen müssen die Werte ohnehin ≥0 sein).

 

Grüße

Comments

Danke sehr! Offensichtlich habe ich mich geirrt.
 :)

Answer 2

Zunächst einmal eine kleine Skizze des Sachverhalts (hilft meistens): 

Wir haben ein rechtwinkliges Dreieck mit der Hypotenuse c und der Information, dass Mast + c = 10 Meter, also

Mast = 10 - c

5^2 + (10 - c)^2 = c^2 

25 + 100 - 20c + c^2 = c^2

125 = 20c

c = 125/20 = 6,25

Da der Mast 10 - c ist, folgt, dass sich die Knickstelle in einer Höhe von 3,75 Metern befindet. 

Probe: 

3,75^2 + 5^2 = 39,0625

6,25^2 = 39,0625

passt :-)

 

Allgemeine Formulierung ist dann: 

x (Höhe der Knickstelle) + c (Länge des abgeknickten Stücks) = h (Höhe des Mastes)

w^2 + x^2 = c^2

x^2 = c^2 - w^2

Jetzt c = h - x eingesetzt:

x^2 = (h - x)^2 - w^2

x^2 = h^2 - 2hx + x^2 - w^2

0 = h^2 - 2hx - w^2

2hx = h^2 - w^2

x = (h^2 - w^2) / (2h)

 

Nicht schön, aber passt ...