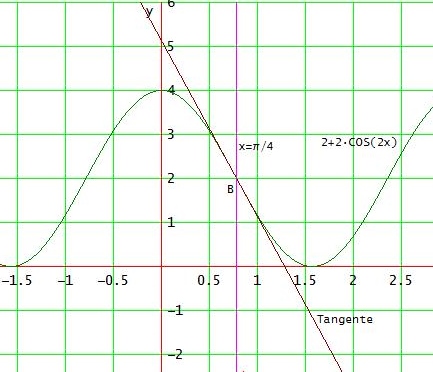
f(x) = 2 + 2 cos(2x) ; x ∈ [ -2 ; 3 ]
die Steigung der Tangente ist m = f '(xB) = -4 , ( || g)
f '(x) = - 4·SIN(2·x) = - 4
sin(2x) = 1
2x = π/2 + k * 2π mit k∈ℤ
x = π/4 + k * π mit k∈ℤ
der einzige Wert für x ∈ [ -2 ; 3 ] ergibt sich mit k = 0:
x = π/4 ≈ 0,785
f(π/4 ) = 2 + 2 cos(2*π/4 ) = 2 → Berührpunkt B( π/4 | 2 )
Die Gerade durch den Punkt P( xp | yp ) mit der Steigung m hat die Gleichung
y = m • ( x - xp ) + yp [ Punkt-Steigungs-Formel ]
Tangentengleichung:
y = -4 *( x - π/4) + 2
y = - 4 x + π+2
Gruß Wolfgang