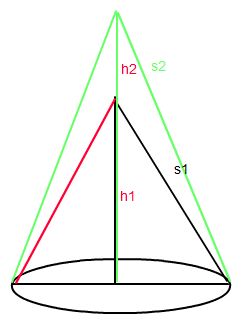
Um s zu bestimmen braucht man die Höhe
V= 1/3 *r²*π *h nach h umstellen und r und V einsetzen
h= (3*321,4)/(π *5,1²)=11,7998≈11,8cm
nach dem Pythagoras ist s
s= √(r²+h²) | r und h einsetzen
s=12,8548≈12,9cm
Neues s = s+ (1/2) s=19,35cm
neue Höhe h=√(19,35²- 5,1²)=18,67
Oberfläche Kegel O = π r*(r+s) Werte von oben nehmen und einsetzen,berechnen
O alt O= 288,39cm² ⇔100%
O neu O=391,74cm² ⇔135,83%
Die Oberfläche vergößert sich um (135,83 -100=35,83) 35,83%.
siehe skizze