Grenzwert von Winkelfunktionen bestimmen. Bsp. lim tan(πx/2) für x→1−

Question

Bestimme die Grenzwerte durch Eigenschaften der Winkelfunktionen:

a) lim tan(πx/2)

x→1−

b) lim tan(πx/2)

 x→1+ 

c) lim 3√x sin(1/x)

x→0

d) lim sin(x²)/x²

x→1

Answer 1

lim tan(πx/2)

x→1−

verwende tan(z) = sin(z) / cos(z)  also

tan(πx/2)  =  sin (πx/2) / cos (πx/2)

für x gegen 1- geht   sin (πx/2)   gegen 1 und 

cos (πx/2)  gegen 0, ist aber vorher positiv, also GW  + ∞

von der anderen Seite - ∞ , weil cos dann negativ.


3√x sin(1/x)   

sin(1/x)  ist beschränkt durch + 1 und -1 und  

3√x  geht gegen 0,  also  GW = 0

d)  GW ist  sin(1) .

Answer 2

zu a) und b)

Tangensfunktion:

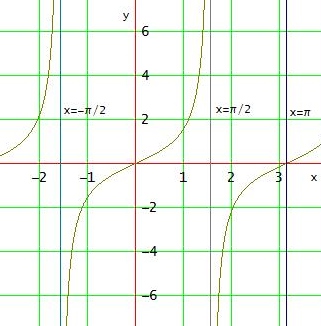
a)

    lim_{x→ 1-}  tan(πx/2) =  ∞

        Das Argument  πx/2 → π/2 (von unten)  für x → 1^-

        Bei stetiger Annäherung des Arguments an π/2 von links strebt der Wert der                       stetigen Tangensfunktion gegen ∞

b) 

    lim_{x→ 1+} tan(πx/2) = - ∞

           Das Argument  πx/2 → π/2  (von oben)  für x → 1⁺

        Bei stetiger Annäherung des Arguments an π/2 von rechts strebt der Wert der                     stetigen Tangensfunktion gegen - ∞

c)

    lim_x→0  [ 3√x sin(1/x) ] = 0

            wegen  -1 ≤ sin(1/x) ≤ 1  und  √x → 0  für x → 0

d)

 lim_{x→ 1}  [ sin(x²)/x² ]  =  sin(1) /1  = sin(1)  ≈ 0,8414709848

          Der Grenzwert der in ℝ \ {0} stetigen Funktion  x ↦ sin(x²)/x²  stimmt mit dem                         Funktionswert an der Stelle x=1 überein.

Gruß Wolfgang