Ungleichung zeichnen x<=x^2

Question

Hi,

wie zeichne ich diese Ungleichung in R^2?

x<=x^2

Comments

Kommt y in der Ungleichung nicht vor? 

Answer 1

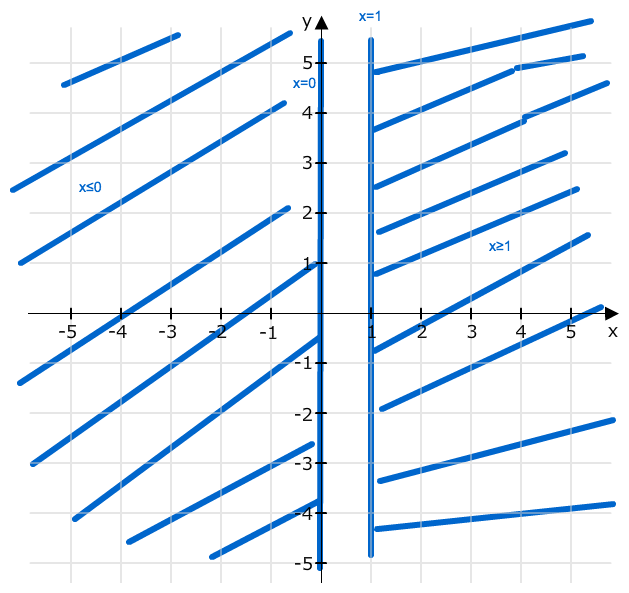
Ohne y in der Ungleichung:

x ≤ x² 

0 ≤ x^2 - x = x(x-1) 

Rechts hast du 0 für x = 0 und x = 1.

Wenn x>1 ist, ist x und (x-1) > 0 und das Produkt auch.

Wenn x<0 ist, ist x und (x-1) < 0 und das Produkt ist grösser als 0. 

Für x zwischen 0 und 1 ist das Produkt kleiner als 0.

Also hast du L = { (x|y) | x≤0 oder x≥ 1 , y beliebig} 

Answer 2

Ich bin mir nicht sicher, aber ist die Lösung nicht einfach, dass du die Funktion Wurzel x zeichnest ?