Ungleichung zeichnen |x+y|<=|x-y|

Question

Hi,

wie zeichne ich diese Ungleichung?

Ich dachte nämlich, dass es sich gegenseitig aufhebt wegen

0<= |x-y|-|x+y|

Answer 1

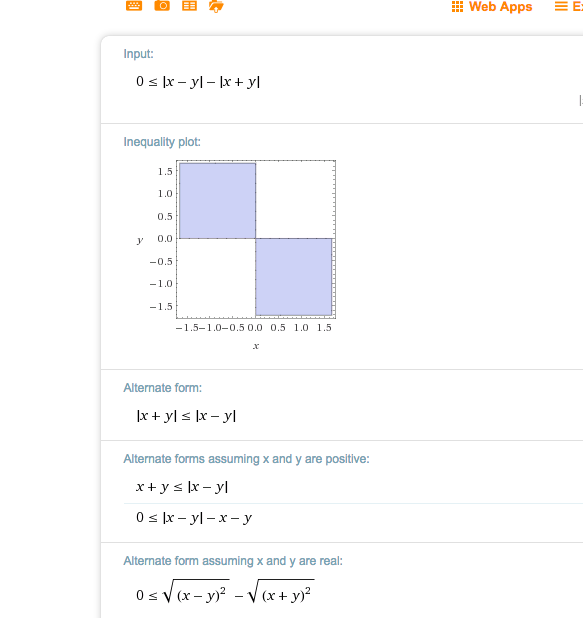
  |x+y| ≤ | x-y| 

Das hebt sich nicht gegenseitig auf.

Wenn du Fallunterscheidungen vermeiden willst, quadrierst du links und rechts:

x^2 + 2xy + y^2 ≤ x^2 - 2xy + y^2          | -x^2 - y^2 + 2xy

4xy ≤ 0       | :4

xy ≤ 0  . Produkt Null oder Negativ. 

L = { (x|y) | x = 0 oder y = 0 oder (x<0 und y>0) oder (x>0 und y <0) } 

Überlege dir mal, wie das nun aussieht:

https://www.wolframalpha.com/input/?i=0%E2%89%A4+%7Cx-y%7C-%7Cx%2By%7C

Answer 2

Schraffiere den zweiten und den vierten Quadranten. Wenn x und y unterschiedliche Vorzeichen haben, ist die Ungleichung grundsäzlich erfüllt. Auch für (0/0).