Funktion einer zylindrischen Dose

Question

Die Höhe h einer zylindrischen Dose beträgt h cm.

-Stelle die Gleichung jener Funktion auf, die den Durchmesser d in Abhängigkeit vom Volumen V beschreibt.

Meine Überlegung:    V(h) = (d² * π * h) / 4

-Beschreibe, wie sich die Höhe h ändert, wenn der Durchmesser d halbiert wird.

?

-Skizziere die Funktion h(d)

?

--------------------------------------------------------------------------------------------------------------

Es wäre nett wenn mir jemand das Beispiel erklärt :)

Answer 1

> Stelle die Gleichung jener Funktion auf, die den Durchmesser d in Abhängigkeit vom Volumen V beschreibt.

V = (d² * π * h) / 4

Du musst nach d umstellen:

d(h)  = 2·√[ V / (π • h) ]  

> Beschreibe, wie sich die Höhe h ändert, wenn der Durchmesser d halbiert wird.

h(d) = 4V / (d² • π) =  (4V / π) • 1/d²  

Wenn man d halbiert (also d/2 für d einsetzt, erhält man die 4-fache Höhe.

> Skizziere die Funktion h(d)

 (4V / π)   soll eine feste Größe sein.

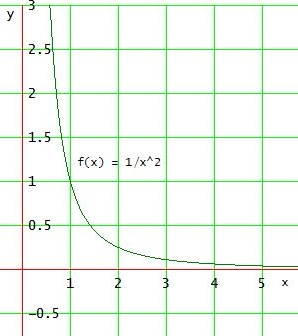
Die Funktion verläuft also  ähnlich wie 1/x²   ( für x>0 )

Gruß Wolfgang