Diskutieren Sie die folgenden Funktionen. Bsp. f(x) = (1-x^2)/(x^2+2x-3)

Question

Diskutieren Sie die folgenden Funktionen (Definitionsbereich, Nullstellen, Polstellen,

Konvergenz und Stetigkeit, Verhalten im Unendlichen) und fertigen Sie mit diesen

Angaben eine Skizze des Funktionsgraphen an.

(a)  f(x) = (1-x²)/(x²+2x-3)

(b) f(x) = (x³+3x²-4x-12)/(x⁴-4x³+16x-16)

Answer 1

Ich gebe dir jetzt einfach mal ein Bild zur Hilfestellung. Zudem gilt für die Polstellen folgende Regel...

Regel zu den Polstellen

An den Stellen, wo die Funktion nicht definiert ist (Nenner null), gibt es zwei Möglichkeiten

1. der Graph besitzt eine behebbare Definitionslücke. Wenn Nullstellen des Nenners auch im Zähler Nullstellen sind

2. der Graph nähert sich immer mehr einer Geraden parallel zur y-Achse an. Diese Gerade nennt man senkrechte Asymptote. Die Definitionslücke heißt dann Unendlichkeitsstelle oder Pol. (Wenn Nullstellen des Nenners keine Nullstellen des Zählers sind.

Answer 2

1)

f(x) = (1-x²) / (x²+2x-3) =  - (x-1) * (x + 1) / [ (x - 1)·(x + 3) ]  

     = _Df   - (x + 1) /(x + 3)  =  -1 + 2/(x + 3)

D_f = ℝ \ { -3 ; 1 }

Nullstelle: x = -1

x = 1 handelt ist eine stetig behebbare Definintionslücke , weil der zugehörige Linearfaktor sich wegkürzen lässt.

lim_x→1 f(x) = 2/4 = 1/2 → Lücke im Punkt ( 1 | 1/2)

x = -3 ist eine Polstelle (senkrechte Asymptote) mit Vorzeichenwechsel, weil der LF nach dem Kürzen in ungerader Potenz stehen bleibt.

Einsetzungen in den offenen Intervallen, die von der Nullstelle und den Definitionslücken begrenzt werden, ergeben den

Vorzeichenverlauf von f:

 x                - ∞              -3            -1              1              ∞ 

 f(x)                         -               +               -               -           

→  lim_{x→ -3-} f(x) = -∞   ;   lim_{x→ -3+}  f(x) = ∞        

limx→±∞ f(x) = -1   ;  f_A(x) = -1  ist die Asymptotenfunktion

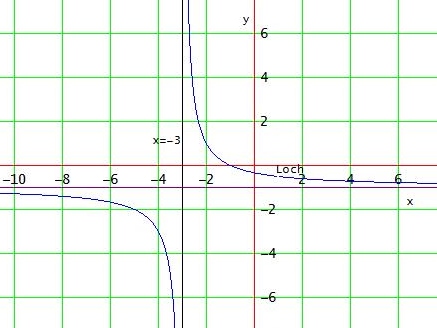
Die obere waagrechte Gerade ist die x-Achse!

2) 

Mit Hilfe der durch Probieren gefundenen Nullstellen von Zähler ( x=2) und Nenner ( x=2  3-fach)

kommt man mit Polynomdivisionen durch die Linearfaktoren zu der Darstellung:

f(x) = (x³+3x²-4x-12) / (x⁴-4x³+16x-16) 

      =  (x + 2)·(x - 2)·(x + 3) / [ (x + 2)·(x - 2)³ ]

      =_Df  (x + 3) / (x - 2)² 

Jetzt kannst du dir oben weitere Anregungen holen.

Gruß Wolfgang