x ² + y ² <= 16 wird erfüllt durch alle Punkte ( x | y ) , die auf dem Rand und innerhalb eines Kreises mit dem Radius 4 um den Ursprung liegen. Diese Punkte bilden die Menge A.
y > √ x wird erfüllt durch alle Punkte ( x | y ) des ersten Quadranten, die oberhalb des Graphen mit der Funktionsgleichung f ( x ) = √ x liegen. Diese Punkte bilden die Menge B. Die Punkte auf dem Graphen von f gehören nicht zur Menge B. Die Punkte auf der positiven y-Achse gehören zur Menge B, wenn R+ auch die 0 enthält, was ich hier annehme.
y > - 1/2 x + 3 wird erfüllt durch alle Punkte, die oberhalb der Geraden mit der Funktionsgleichung g ( x ) = - 1/2 x + 3 liegen. Diese Punkte bilden die Menge C. Die Punkte auf der Geraden gehören nicht zu C.
y >= x ² wird erfüllt durch alle Punkte ( x | y ), die auf und oberhalb der Parabel mit der Funktionsgleichung p ( x ) = x ² liegen, die also von den Parabelästen umschlossen werden. Diese Punkte bilden die Menge D.
Die Schnittmenge S = A ∩ B ∩ C ∩ D besteht nun aus all denjenigen Punkten der Mengen A, B, C, D, die alle der genannten Bedingungen erfüllen.
Hier eine (schlechte) Skizze, die Menge S ist rot markiert:
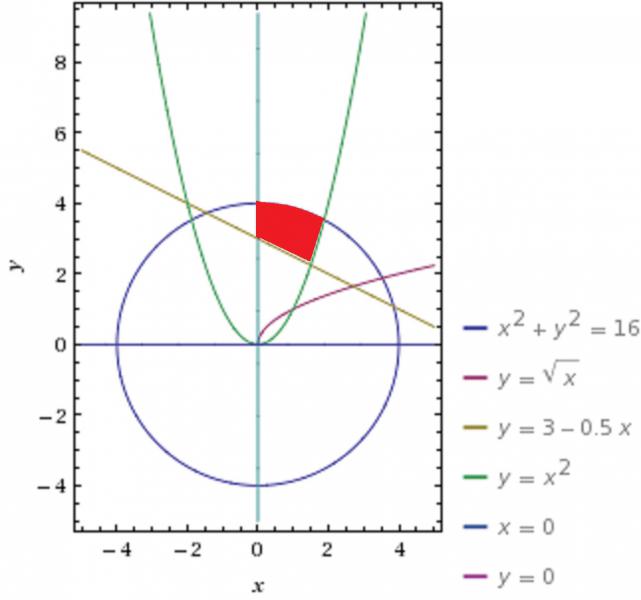
(Hinweis: Ich habe die Zeichnung mit WolframAlpha erstellt und musste dabei das Koordinatensystem durch die Graphen zu x = 0 und y = 0 selbst erzeugen, da WA das einfach nicht tun wollte :-) )
b) Sei M die Menge aller Punkte ( x | y ) ∈ S für die gilt, das x und y natürliche Zahlen einschließlich der 0 sind, dann enthält M, wie man aus der Skizze entnehmen kann, nur die Punkte ( 0 | 4 ) und ( 1 | 3 ). Der Punkt ( 0 | 3 ) etwa gehört nicht zu M, da er nicht zur Menge C und damit nicht zur Schnittmenge der Mengen A, B, C und D gehört.