Die Menge B ist eine Kreisscheibe mit Rand.
Mittelpunkt der Kreisscheibe aus der Gleichung ablesen M(-1|0) .
Radius der Kreisscheibe r = √(9) = 3
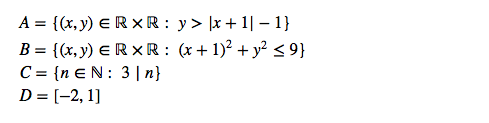
A: Zeichne erst den Funktionsgraphen von f(x) = |x+1| - 1 und markiere dann alles oberhalb von diesem Graphen.
C: Alle natürlichen durch drei teilbaren Zahlen: 0,3,6,9,…
D: Das Intervall [-2,1]
a) Skizzieren Sie die Menge (A geschnitten mit B) vereinigt mit (DxD).
DxD ist ein achsenparalleles Quadrat. Das Intervall D ist auf beiden Achsen einzuzeichnen. Dann zum Quadrat ergänzen. AnB kannst du selbst einzeichnen (?). Dann die beiden Mengen noch vereinigen (zusammenfügen).
b) Skizzieren Sie (DxC) und bestimmen Sie die Menge (DxC) geschnitten mit (A geschnitten mit B).
(DxC) . D auf der x-Achse und C auf der y-Achse einzeichnen. Es ergeben sich horizontale Strecken der Länge 3 .
Dann noch diejenigen Teile der Strecken auswählen, die in AnB liegen.