Vom Duplikat:
Titel: Gegeben sei die Matrixgleichung A·X + B·X = C mit den Matrizen
Stichworte: determinante,matrixgleichung,matrix
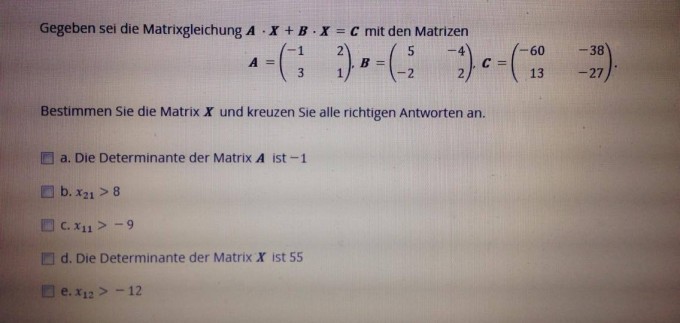
Kann mir bitte bitte jemand sagen wie diese Aufgabe zu rechnen geht bzw. mir den Rechenweg zeigt. Beschaeftuge mich erst seit Kurzem mit diesem Thema und deswegen leider fast gar nicht mit dem vertraut...