Bestimmen sie den Faktor a so, dass schraffierter Flächeninhalt 1,6cm² beträgt?

Question

Hey

Aufgabenstellung:

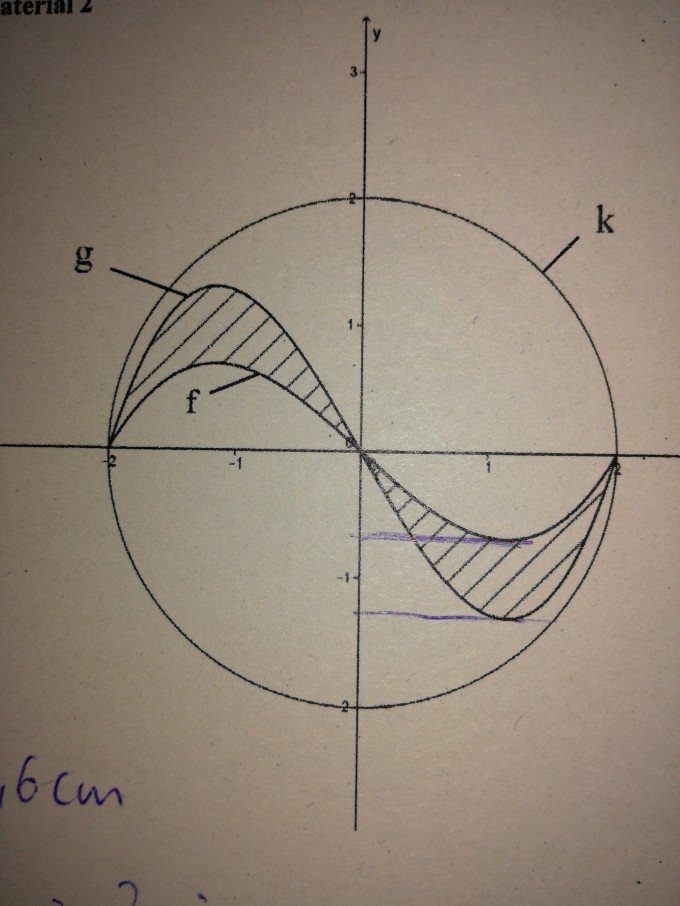
Bei einer zweiten Variantw der Brosche wird zusätzlich zu der durch f gegebenen Linie eine zweite Linie angebracht, die durch eine Funktion g mit

g(x)= a* f(x), a>1

beschrieben werden kann.

Bestimmen sie den Faktor a so, dass der schraffierte Flächeninhalt 1,6cm² beträgt.

Funktion f haben wir schon bestimmt:

f(x)= 2/9 x³ -8/9 x

Mein Lösungsansatz:

Differenzenfunktion bestimmen

f(x) = g(x)

2/9 x³ -8/9 x = ax³ -8/9x

2/9 x³ = ax³

h(x)= 2/9x³ -ax³

Dann Integral anwenden:

O.8 = ₀∫² (2/9 x³ -ax³)dx

=[1/18 x⁴ - a/4 x⁴ ]

Und ab hier weiß ich nicht mehr wies weitergehen soll

Ich hab in die Stammfunktion dann die 2 eingesetzt und nach a aufgelöst aber dann kam da -1/45 raus was eingezeichnet voll falsch aussah?

Danke für alle Antworten :)

Comments

Ich glaub ich hab die Differenzenfunktion falsch bestimmt, aber ich weiß auch nicht wie ich das mit dem a machen soll :(

Answer 1

> f(x)= 2/9 x³ - 8/9 x  und   g(x) = a* f(x) ; a>1

der Graph von f ist symmetrisch zum Ursprung

A =  2 * _-2∫⁰ (g(x) - f(x)) dx  =  2 * _-2∫⁰ (a*f(x) - f(x)) dx  = 2 * ₂∫⁰ (a-1) * f(x) dx

    =  2 * (a-1) * _-2∫⁰  f(x) dx  =  2 * (a-1) * _-2∫⁰ (1/18 x⁴ - 4/9 x²) dx

    =   2/9 * (a-1) * [ 1/2 x⁴ - 4 x² ]_-2⁰  =  2/9 * (a-1) * ( 0 - (8 - 16)

    =  2/9 * (a-1) * 8  =  16/9 * (a-1)

Fläche = 1,6 cm²

16/9 * (a-1) = 1,6   ⇔  a-1 = 1,6 * 9/16  ⇔  a = 1,6 * 9/16 + 1

⇔  a  =  19/10  =  1,9

Gruß Wolfgang

Comments

Danke Wolfgang, auf dich kann man sich immer verlassen :D <3