Steigung berechnen und Gerade Zeichnen. (1|1) (-2|0) - Wo ist der Schnittpunkt?

Question

Aufgabenstellung:

Eine Gerade geht im Koordinatensystem durch die Punkte (1|1) und (-2|0). Wie lautet ihre Gleichung? Wie groß ist ihre Steigung? Wo schneit die Gerade die beiden Koordinatenachsen? Bitte rechnen und zeichnen Sie!

Problembeschreibung:

Die Gleichung habe ich schon. Hier ist mein Versuch bei der Berechnung der Steigung und dem Zeichnen:

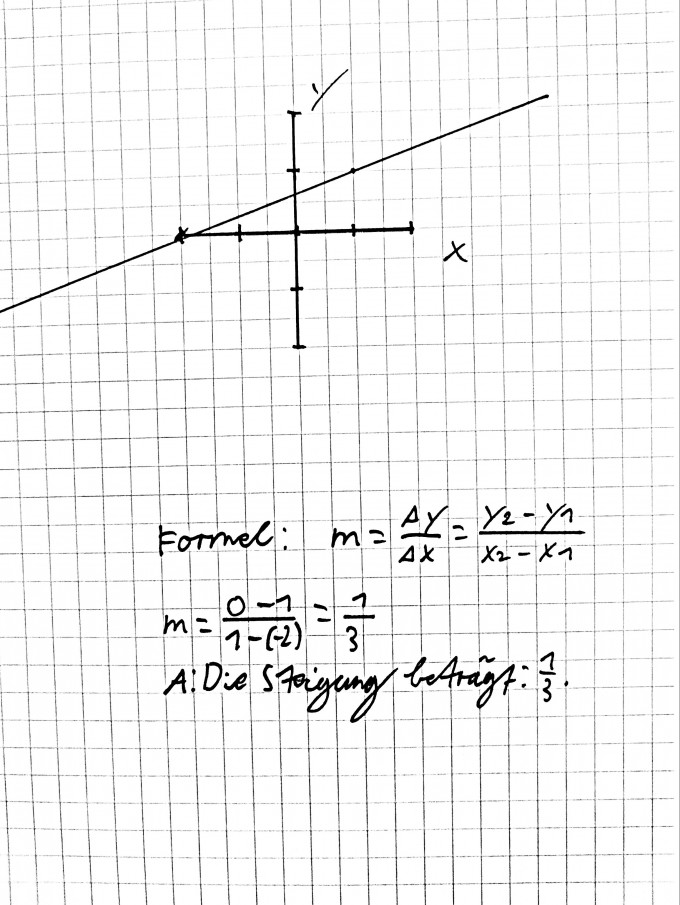
Wie "berechne" / lese ich denn nun die Schnittpunkte ab? auf der X-Achse wäre es dann -2 (sofern ich richtig gezeichnet hätte) und auf der Y-Achse .. 0,7?

Comments

Mit deiner Rechnung stimmt was nicht. So wie du das aufgeschrieben hast käme da die Steigung -1/3 raus. überprüfe das nochmal!

---

Da hast du natürlich recht. Dennoch finde ich den Fehler nicht. Y werte von (1|1) und (-2|0) sind laut dieser Formel so wie ich es aufgeschrieben habe (glaube ich). Mit einer negativen Steigung würde das eingezeichnete aber nicht stimmen. Wobei ich einfach nur die Koordinaten eingezeichnet habe.

Eine Idee wo mein Fehler liegt? Oder habe ich eine falsche Formel genommen?

https://de.wikipedia.org/wiki/Steigung

---

Die Formel stimmt. Du musst einmal festlegen welcher Punkt der mit dem Index 1 ist und welcher der mit dem Index 2. sodann ergibt sich m=(0-1)/(-2-1)=-1/-3=1/3

---

Wie kommst du denn auf -1/-3=1/3. Darf man das bei Ergebnissen von Steigungen?  Oder ist das einfach irrelevant, da es von dem Ausgangspunkt abhängt?  Sprich wenn man am höchsten punkt ansetzt wäre es eine "Senkung" und vom niedrigsten eine "Steigung" 

---

Wenn man ein bruch hat wo oben und unten ein Minus steht, dann darf man das minus erstmal kürzen. Dadurch hat man dann einen positiven bruch. Ist der bruch positiv dann ist auch die steigung positiv ("es geht nach oben") und ist der bruch negativ, dann ist auch die steigung negativ, man hat also ein Gefälle ("es geht nach uhten"). Das hat nichts damit zu tun, von wo aus man guckt.

Answer 1

Strahlensatz 2/b=3/1 b=2/3 (etwas weniger als 0,7.