Quadratischen Funktionen: g(x)=0,5x²-mx+3 – Bestimme m so, dass die Funktion g mindestens 1 Nullstelle besitzt.

Question

Gegeben ist die Funktion g durch g(x)=0,5x²-mx+3

Bestimmen Sie m so, dass die Funktion g mindestens 1 Nullstelle besitzt.

ich weiß zwar das man die Aufgabe mithilfe der Mitternachtsformel lösen kann weiß allerdings nicht wie ich den Parameter m interpretieren soll. Es wäre sehr nett wenn jemand die Aufgabe lösen könnte und mir dann die Antwort mit Erklärung schreiben würde damit ich solche Aufgaben in der Matheschulaufgabe richtig lösen kann.

Answer 1

g(x)=0,5x²-mx+3  = 0 

gibt mit der Formelx = (  m ±√ ( m² - 4 * 0,5 * 3 )  /  1

= (  m ±√ ( m² - 6 )  /  1Damit man die Wurzel ausrechnen kann, darf

in der Wurzel nichts negatives stehen, also mussb² - 6 ≥ 0    sein,  also     b²   ≥  6und damit b   ≤ - √6    oder    b   ≥   √6   sein.

Answer 2

Funktionsterm 0 setzen und alles mit 2 multiplizieren ergibt: x²-2m+6=0. pq-Formel x=m±√(m²-6). Der Term unter der Wurzel entscheidet über die Anzahl der Lösungen: m²-6≥0 oder m²≥6. m darf also nicht zwischen -√6  und +√6 liegen.

Answer 3

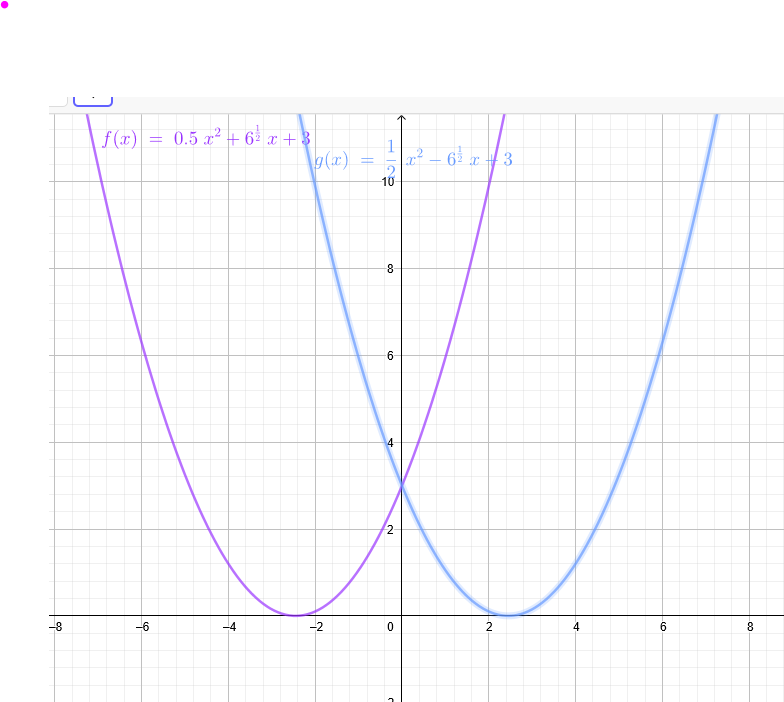
g(x)=0,5x²-m*x+3

g´(x)=x-m

x-m=0     m=x

Ortslinie für die Tiefpunkte der Parabel: o(x)=-0,5x^2+3

Nullstellen der Ortslinie:

-0,5x^2+3=0    \(x₁=- \sqrt{6} \)    \(x₂= \sqrt{6} \)

1.)\(g(- \sqrt{6})=0,5*6+ \sqrt{6}*m+3\)

\(6+ \sqrt{6}*m=0\)         \(m=- \sqrt{6}\)

2.)\(g( \sqrt{6})=0,5*6- \sqrt{6}*m+3\)

\(6- \sqrt{6}*m=0\)        \(m= \sqrt{6}\)

Answer 4

f(x) = 0.5·x^2 - m·x + 3 = 0

Mitternachtsformel ist prima. Du weist, dass die Diskriminante (also das unter der Wurzel) größer gleich null ist, damit es mind. eine Lösung gibt.

D = b^2 - 4·a·c = (- m)^2 - 4·(0.5)·(3) ≥ 0 --> m ≤ - √6 ∨ m ≥ √6

Und das ist dann bereits die Lösung.