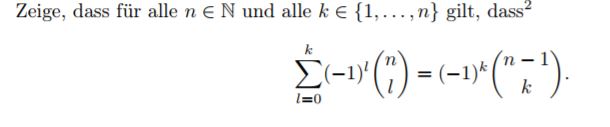Zeigen Sie fur alle n ∈ N0, x ∈ R alternierende Summe von Binomialkoeffizienten = ...

Question

Zeigen Sie fur alle  n ∈ N0, x ∈ R

$$ \sum _{ k=0 }^{ n }{ { (-1) }^{ k } } (\begin{matrix} x \\ k \end{matrix})=({ -1) }^{ n }(\begin{matrix} x-1 \\ n \end{matrix}) $$

Ich gehe mal davon aus das dies am besten per Induktion zu zeigen ist, allerdings habe ich so meine

Probleme mit dem Term.

Comments

Schau mal bei den ähnlichen Fragen. Bsp https://www.mathelounge.de/390592/alternierende-binomialkoeffizienten-beweisen-ergebnis

Unterschied zum Teil wohl, dass dein x nicht aus N ist.

---

Links und rechts stehen Polynome n-ten Grades in x. Die Formel stimmt für x=0, x=1, ..., x=n (vgl. Kommentar oben). Nach dem Identitaetssatz für Polynome sind beide Seiten für alle x gleich.

---

Vom Duplikat:

Titel: Induktion über eine alternierende Summe mit n über k

Stichworte: binomialkoeffizient,summe,alternierend,vollständige-induktion

habe mal eine Frage zu dieser Aufgabe.
den Beweis gebe ich in einer vollständigen Induktion an.
beim Induktionsanfang setzt man ja n=1 
jedoch stand bis jetzt auf der Summe oben immer ein n und hier nun ein k
kann ich jetzt für das k= n+1 einsetzen oder gehe ich da einen falschen Weg?

---

Ist das nicht (im Prinzip) diese Frage https://www.mathelounge.de/400125/zeigen-sie-alle-alternierende-summe-binomialkoeffizienten ?

---

praktisch ja aber diese beantworten meine Frage leider auch nicht

---

Frage vielleicht mal bei fakename nach, was du dort nicht verstehst.

---

"kann ich jetzt für das k= n+1 einsetzen oder gehe ich da einen falschen Weg? "

Nein. Das darfst du nicht. k ist ausdrücklich eine beliebige natürliche Zahl von 1 bis n. Daher ist n+1 nicht möglich. 

---

Frage vielleicht mal bei fakename nach, was du dort nicht verstehst.

F behauptet doch genau das was hier zu beweisen ist und beruft sich dabei auf einen Kommentar, der nur den Fall k=n behandelt, also ist doch der Kommentar " diese beantworten meine Frage leider auch nicht " vollkommen berechtigt.

---

Nachfragen und den Beantworter auf einen möglichen Fehler hinweisen, schadet ja nicht.

---

Schau dir mal die Diskussion hier an: https://www.mathelounge.de/481363/induktion-uber-eine-alternierende-summe-mit-n-uber-k#c481371

---

Bei der anderen Antwort ging es darum, wie man aus für alle n∈ℕ auf für alle x∈ℝ schliesst. Die Formel für n∈ℕ muss man dazu natuerlich schon haben. Der dort angegebene Link auf eine aeltere Frage passt aber tatsaechlich nicht. Wird aber auch passende Links geben. :)

Oder selber eine Induktion nach n machen ...