144 Steine in 36 Farben, jeweils 4 gleichfarbige Steine in eine Reihe gelegt. Wie viele Kombinationen sind möglich?

Question

144 Spielsteine in 36 Farben, jeweils 4 gleichfarbige Spielsteine in eine Reihe gelegt. Wieviele Kombinationen sind möglich?

Answer 1

 

auch wenn die Frage schon etwas länger her ist, möchte ich sie an dieser Stelle beantworten, um zukünftigen Lesern zu helfen.

Aus der Aufgabenstellung lese ich heraus, dass die insgesamt \(144\) Spielsteine in Gruppen zu je \(4\) gleichfarbigen Steinen in eine Reihe gelegt werden. Das sähe in etwa so aus:

  

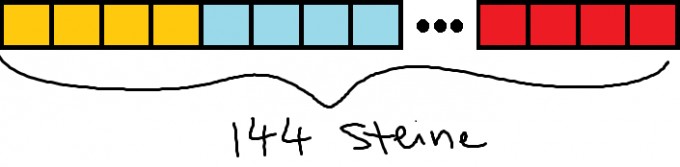
Passenderweise ist \(144 = 36\cdot 4\). Da die 4 Farben in jeweils zusammenhängenden Gruppen/Reihen aneinandergelegt werden, ergeben sich $$36!$$ Möglichkeiten. Wenn allerdings nicht alle \(144\) Steine genutzt werden sollen, sie jedoch in Vierergruppen zusammengelegt werden müssen, sind das $$\sum_{k=1}^{36}{\binom{36}{k}\cdot k!}$$ mögliche "Farbcodes", die aus jeweils \(4k\) Steinen bestehen.

Wenn das Szenario anders gemeint war, kannst Du Dich gerne noch einmal melden.

André, savest8

Comments

Danke für die Antwort.

Die Frage war nicht exakt gestellt.

Ausgangslage: 144 Spielsteine, jeweils 4 gleichfarbige Steine  in 36 verschiedenen Farben.

Gemeint war: Wenn ich alle 144 Steine beliebig (nicht zwingend in Farbgruppen, wie in Ihrer Lösung) in eine Reihe auslege, wie viele Farbkombinationen (Muster) sind möglich?

Arthur Heger

Answer 2

$$ {144! \over 4! \cdot 4! \cdot 4! \cdots 4!} = {144! \over (4!)^{36}} = 1.14\cdot10^{200} $$