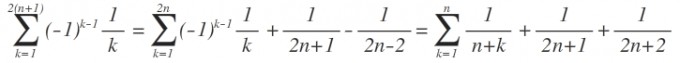Induktion: alternierende harm. Reihe

Question

Hallo !

Ich versuche nun seit einiger Zeit hinter das Geheimnis des Beweises zu kommen. Scheitere aber kläglich !

Es geht darum, dass ich folgendes im Induktionsschritt beweisen möchte:

 

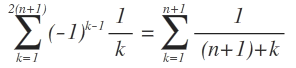
Bei mir sieht das bis jetzt wie folgt aus:

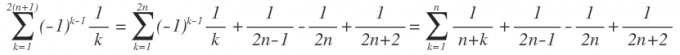
Hier habe ich die Summe bis 2n und dann plus (n+1) dargestellt. Liegt hier vielleicht mein Fehler ?

In der Lösung, die mir vorliegt, sieht das ganze allerdings anders aus, wenn die Summe bis 2n dargestellt wird :-/

So steht es in der Lösung:

Answer 1

$$  \sum_{k=1}^{2(n+1)}{{(-1)}^{k-1}*\frac { 1 }{ k}}$$

$$  = \sum_{k=1}^{2n+2}{{(-1)}^{k-1}*\frac { 1 }{ k}}$$Es folgen also nach der Summe bis n noch zwei Summanden:$$  = \sum_{k=1}^{2n}{{(-1)}^{k-1}*\frac { 1 }{ k}}  + {{(-1)}^{2n}*\frac { 1 }{ 2n+1}} + {{(-1)}^{2n+1}*\frac { 1 }{ 2n+2}} $$

Und die (-1) Potenzen liefern einmal + und einmal -$$  = \sum_{k=1}^{2n}{{(-1)}^{k-1}*\frac { 1 }{ k}}  +\frac { 1 }{ 2n+1} - \frac { 1 }{ 2n+2} $$

und daraus wird dann

$$  = \sum_{k=1}^{2n}{{(-1)}^{k-1}*\frac { 1 }{ k}}  +\frac { 1 }{ 2n+1} + \frac { 1 }{  -2n - 2} $$Da fehlt wohl ein "minus" vor den 2n im Nenner.