Bestimmen bei der Gegebenen Reihe die Partialsumme bzw. den zugehörigen Grenzwert

Question

ich rätsel bei folgender Aufgabe immer noch an der Lösung von meinem Professor. Also die Aufgabe ist folgende:

Bestimmen bei der Gegebenen Reihe die Partialsumme bzw. den zugehörigen Grenzwert

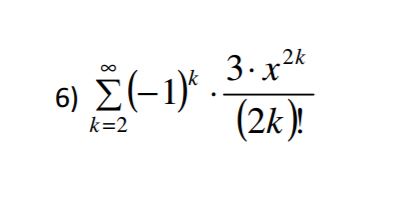
So und das hier ist die Lösung von meinem Professor

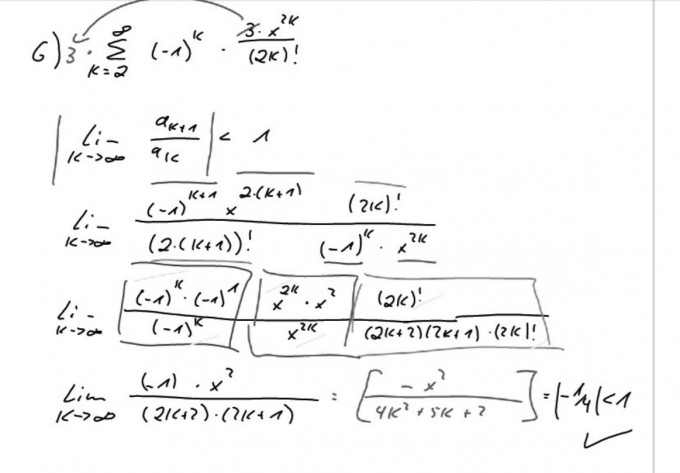
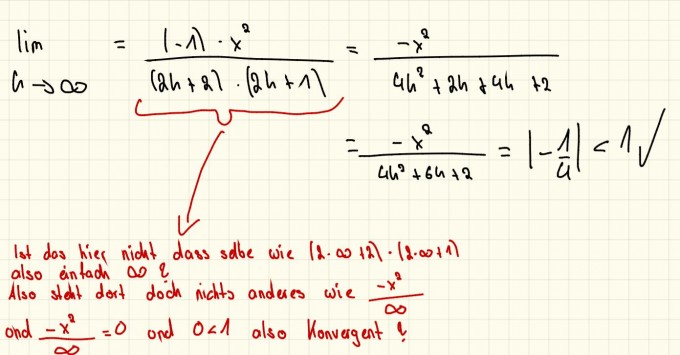
Ich verstehe aber den letzten Schritt nicht.  Das sind doch 4K^2 *6K +2 und wie kommt man dann überhaupt auf die -1/4.

Wird außerdem (2k+2) * (2k+1) nicht einfach unendlich`? Siehe meine Frage im nächsten Bild

Answer 1

Ich kann mir das eigentlich nur so erklären, dass gleichzeitig k gegen unendlich

und x gegen unendlich betrachtet wird. Sozusagen beide identifiziert

werden, dann ist natürlich   der Grenzwert für  x gegen unendlich  von

- x² /  (  4x² + x + 2 )  =  -  1  /  (  4 + 1/x + 2/  x²  ) und das geht gegen   -1 / (  4 + 0 + 0 )   =  -1 / 4

Answer 2

für ein festes x konvergiert die Reihe immer.

Im Beispiel wurde x=k gesetzt, dann konvergiert die Reihe immer noch. Weshalb das getan wurde weiß ich nicht ;)