Beides ist falsch.
Für die Berechnung der Anzahl N der Reihen gehst Du wahrscheinlich von folgender Gleichung aus: $$\sum_{i=0}^{N-1} \left( 40-2i \right) =400$$ Das führt zu einer quadratischen Gleichung mit den Lösungen \( N_1=16\) und \(N_2=25\). Die Begründung für die Existenz einer zweiten Lösung liegt darin, dass der Summand der Summenformel bei ausreichend großem i negativ wird. D.h. die Summe der benötigten Schindeln steigt an, bis eine Reihe mit 0 Schindeln erscheint und danach fällt die Summe rein nummerisch wieder ab!
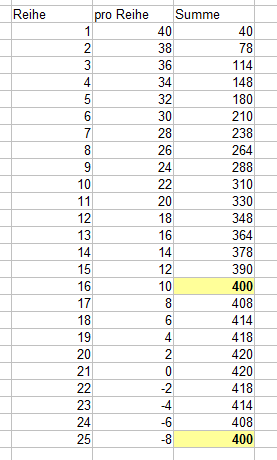
Da Du keine Reihen mit einer negativen Anzahl von Schindeln legen kannst, fällt die zweite Lösung unter den Tisch. Die folgende Tabelle zeigt es direkt:
Gruß Werner