Darstellung von sin(x) als x-x^3/3!

Question

kann man die Funktion sin(x) als x-x^3/3! darstellen? bin darüber gestolpert aber nicht ganz sicher ob das stimmt.Gilt das gleiche dann auch für cos(x) ? -> 1-x^2/2!danke schonmal

Answer 1

Hallo Lukas,

Der Ausdruck \(x-\frac{x^3}{6}\) ist der Beginn der Taylorreihe für die Sinus-Funktion um den Punkt \(x=0\). Von daher ist der Ausdruck nicht identisch zu \(\sin x\), aber eine gute Näherung in der Nähe von \(x=0\).

Das gleiche gilt für \(\cos x \approx 1 - \frac{x^2}{2}\); wieder nur in der Nähe von \(x=0\).

 

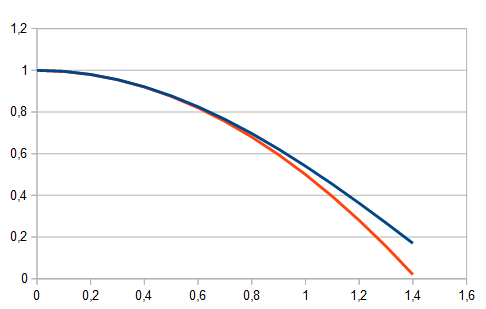
In diesem Bild siehst Du den Cosinus und seine Näherung über einander. Der Cosinus ist die blaue und die Näherung ist die orange Kurve.

Gruß Werner